(Eは平均値０の分布)という比例分散モデルに対して、
(eは平均値Bの分布)と考えれば、
となるので、 広義の乗法モデル と言えます。
筆者が、比例分散モデルの話をした時に、「乗法モデルと同じですね。」と、コメントをいただいたことがあります。
確かにそうなのですが、「同じ」ということが、どうやら２つあります。
ひとつは、広義の乗法モデルとの関わりで、比例分散モデルが広義の乗法モデルの一種という点です。 乗法モデル のページの説明で言うと、比例分散モデルは、広義の乗法モデルです。
もうひとつは、狭義の乗法モデルとの関わりで、狭義の乗法モデルと比例分散モデルで、同じようなグラフになることがある点です。
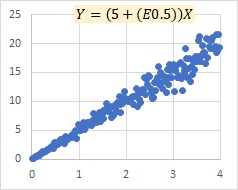
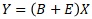(Eは平均値０の分布)
という比例分散モデルに対して、
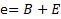(eは平均値Bの分布)
と考えれば、
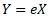
となるので、
広義の乗法モデル
と言えます。
比例比例分散モデル にも同じことを書いていますが、数学的には乗法モデルで表現できても、実務上では、比例分散モデルは、加法モデルの形で考えた方が良いと思います。 加法モデルの形だと、グラフの中で、傾きとして見える部分と、ばらつきとして見える部分を分解して考察できるためです。
狭義の乗法モデルというのは、Eが平均値が０になっているモデルです。 比例分散モデルも、Eは平均値が０を想定しているモデルです。
乗法モデルexp(E)と比例分散モデルは、ほとんど変わらないような時と、明らかに違う時があります。
ほとんど変わらない時が下の場合で、左が乗法モデルexp(E)で、右が比例分散モデルです。
ここで、Eというのは、残差のばらつきを表していて、例えば、E0.5というのは、「平均値が０、標準偏差が0.5の正規分布」です。
正規分布以外でも同様です。
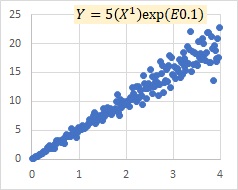
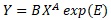
は、 乗法モデルexp(E)のシンプルな形です。
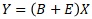
は、 比例分散モデルのシンプルな形です。
Eが小さい時は、乗法モデルexp(E)は、exp(E)がほぼ１になり、比例分散モデルはEがほぼ０になるので、いずれも
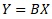
に近くなり、両者は似て来ます。
Eが大きい時は、違いが大きくなります。左が乗法モデルexp(E)で、右が比例分散モデルです。
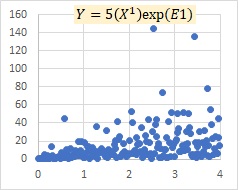
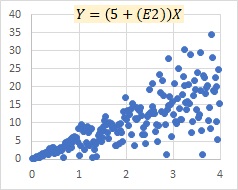
Eが大きい時に違いがでるポイントは、２つあります。 ひとつは、 exp(E) と、Eの違いで、Eが正規分布だと、exp(E)は、裾野が極端に長い分布になることによる違いがあります。
もうひとつは、式の形による違いです。乗法モデルは、３つの要素の掛け算になっていて、比例分散モデルは、BとX、EとXの２つの掛け算を足し合わせた形になっていることからできる違いです。 乗法モデルは、Eが大きいと、BやXの値があまり関係なくなり、Eの影響で決まってきます。 比例分散モデルの方は、Eが大きかったとしても、XとYの比例関係は残ります。
ばらつきが大きくなった時に、乗法モデルexp(E)の場合は、X軸（Y=0）にデータが貼り付くような感じになります。 一方、比例分散モデルの場合は、X軸の近くは、それほど密度が高くなりません。 比例分散モデルの場合は、傾いた直線も周りの密度が高くなります。
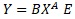
は、乗法モデルEのシンプルな形です。
比例分散モデルで、傾きの項が０の場合、乗法モデルEと比例分散モデルは同じになります。左が乗法モデルexp(E)で、右が比例分散モデルです。
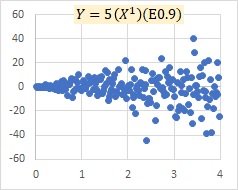
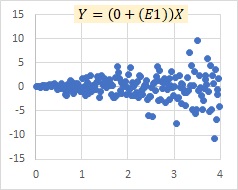
傾きが大きくなると、上記のように乗法モデルexp(E)と、比例分散モデルは似て来ることがありますが、乗法モデルEは比例分散モデルのような傾きを持ったモデルにならないです。
狭義の乗法モデルは、時系列解析のモデルとしてよく知られていて、 Xを時間と考えて、時間が経つほど不確定性が増大することを表現するモデルとして採用されるようです。
比例分散モデルが合う例は、測定器の値をXとした時のモデルです。 自然現象とその測定の関係を扱う時に適しているようです。
順路
次は
加法モデル的乗法モデル
