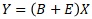(E is a distribution with an average value of 0)For the proportional variance model,
if we consider
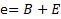(e is the distribution of the mean value B)then
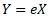
It can be said "Multiplicative model in a broad sense.
When I talked about the Proportional variance model, I received a comment, "It's the same as the Multiplicative model."
That's true, but apparently there are two things that are "the same".
The first is related to the multiplicative model in a broad sense, and the proportional distribution model is a type of multiplicative model in a broad sense. In the description of the Multiplicative Models page, a proportional distribution model is a multiplicative model in a broad sense.
The other is the relationship with the narrowly defined multiplicative model, where the narrowly sensed multiplicative model and the proportional variance model can produce similar graphs.
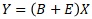(E is a distribution with an average value of 0)
For the proportional variance model,
if we consider
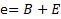(e is the distribution of the mean value B)
then
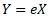
It can be said "Multiplicative model in a broad sense.
Even if it can be expressed mathematically as a multiplicative model, in practice, I think it is better to think of the proportional variance model in the form of an additive model. This is because in the form of an additive model, it is possible to decompose and consider the parts of the graph that appear as slopes and parts that appear as variations.
A multiplicative model in a narrow sense is a model in which E has an average value of 0. The proportional variance model is also a model in which E assumes a mean value of 0.
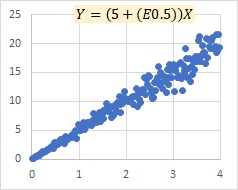
There are times when the multiplicative model exp(E) and the proportional variance model seem to be almost the same, and there are times when they are clearly different. The case below is the time when there is almost no change, the left is the multiplicative model exp(E), and the right is the proportional distribution model.
Here, E represents the variation of the residuals, for example, E0.5 is "a normal distribution with a mean value of 0 and a standard deviation of 0.5". The same is true for non-normal distributions.
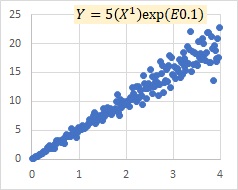
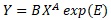
is a simple form of the multiplicative model exp(E).
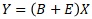
is a simple form of the proportional distribution model.
When E is small, the multiplicative model exp(E) is close to , and the proportional distribution model is close to , because exp(E) is almost 1, and E is almost 0.
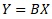
for the proportional variance model.
When E is large, the difference is greater. On the left is the multiplicative model exp(E) and on the right is the proportional variance model.
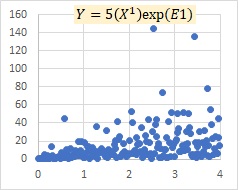
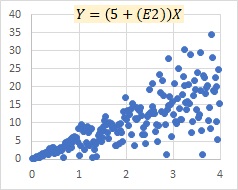
There are two points where the difference can be made when E is large. One is the difference between exp(E) and E, and if E is normally distributed, there is a difference that exp (E) has an extremely long distribution.
The other is the difference in the form of the formula. The difference is that the multiplication model is the multiplication of three elements, and the proportional variance model is the sum of two multiplications: B and X and E and X. In the multiplicative model, when E is large, the values of B and X are not very relevant, and they are determined by the influence of E. In the proportional distribution model, even if E is large, the proportionality of X and Y remains.
When the variation increases, in the case of the multiplicative model exp(E), it feels like the data is stuck on the X axis (Y = 0). On the other hand, in the case of a proportionally distributed model, the density is not as high near the X-axis. In the case of a proportionally distributed model, the tilted straight line is also denser around it.
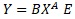
is a simple form of the multiplicative model E.
In a proportional variance model, if the slope term is 0, the multiplicative model E and the proportional variance model are the same. On the left is the multiplicative model exp(E) and on the right is the proportional variance model.
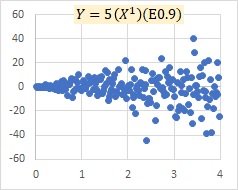
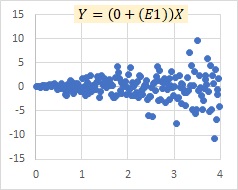
As the slope increases, the multiplicative model exp(E) and the proportional distribution model may become similar as described above, but the multiplicative model E does not become a model with a slope like the proportional variance model.
The multiplicative model in a narrow sense is well known as a model for time series analysis. It seems to be adopted as a model that considers X as time and expresses that the uncertainty increases as time passes.
An example of a proportional variance model is a model when the value of the measuring instrument is X. It seems to be suitable when dealing with the relationship between natural phenomena and their measurements.
NEXT 
Additive model like multiplicative model
