量的変数の相関性の指標は、 相関係数 があります。
連関係数は、相関係数と同じようにして、 質的変数の相関性を分析をするための指標になります。
量的データについては、すべての変数の組み合わせの相関係数を計算して、行列の形にした「相関行列」がよく知られています。
これと同じように質的データについてはも、すべての変数の組み合わせを計算して、連関係数の行列を作るアイディアがあります。
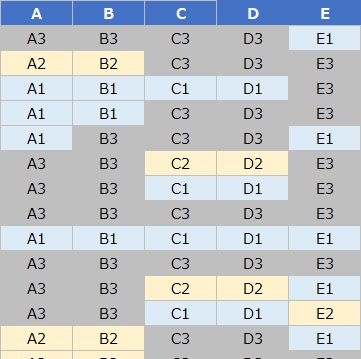
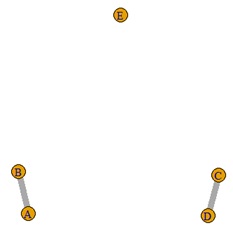
下記は、分析例です。
左がデータ、右が分析結果です。
AとB、CとDの組合せがあることがデータから推測できますが、それをグラフで表現できています。
ちなみに、同じデータを カテゴリの類似度の分析 で分析した結果は、 カテゴリの分解分析 のページにあります。
連関係数は、扱っているのが質的変数なので、線形でないものでも扱えます。
そのため、 量的データを質的データに変換 をすれば、量的変数の非線形な相関性を調べる方法として使うことができます。
ただし、量的なデータの細かさがなくなるので、数値的には粗い調べ方になります。
上のグラフは、 Rによる連関係数分析 で作っています。
R-EDA1
の実施例は、下記です。上図と同じコードがベースです。
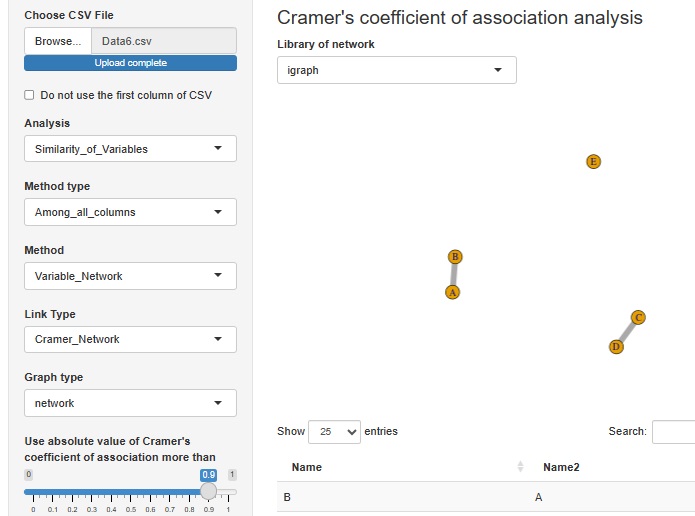
Natto
の「グローバル」という方法は、質的変数の相関性を調べる方法になっています。
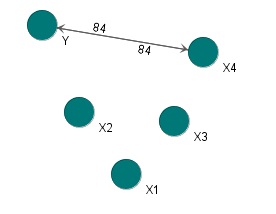
ちなみに、Nattoは、 アソシエーション分析 （ カテゴリの類似度の分析 ）もできるようになっています。
「統計解析ハンドブック」 武藤真介 著 朝倉書店 1995
ユールの連関係数 Q = (ad - bc) / (ad + bc)
Φ係数（四分点相関係数・点相関係数）、ピアソンの連関係数 クラメールの連関係数
「カテゴリカルデータ解析 Rで学ぶデータサイエンス」 藤井良宜 著 共立出版 2014
指標は、ピアソンの一致性係数、クラメールのV統計量。
一般化マンテル検定、クラスカルワリス検定、マクマネー検定、オッズ比の均一性の検定など。
「調査法講義」 豊田秀樹 著 朝倉書店 1998
連関指標として、
比率の差d = a/(a+c)-b(b+d)
、ユール、四分点相関係数を紹介。
共通原因がある場合、第３の変数で層別してから、相関を確認すると良い。
「多変量データ解析法 理論と応用」 柳井晴夫 著 朝倉書店 1994
φは-1から1となり、ファイ相関係数や、点相関係数と呼ばれる。
「R 大量のカテゴリ変数から変数間の連関度を表すクラメールV指標を計算し、有意で連関があるペアのみ抽出する」 武田祐子 氏 2016
https://qiita.com/ytakeda/items/058e83ebdd721f87ceb4
すべての組み合わせについて、
分割表
の形にデータを変換してから連関係数を計算する方法が紹介されています。
順路
次は
連関係数を使った主成分分析
