相互情報量 は、最小値はいつでも０なのですが、最大値はカテゴリの数に依存します。
相関係数や寄与率のように、「絶対値が0から1の間」という決まり方をしないため、関係の強さの指標としては使いにくいです。
このページの相互情報量係数は、いつでも「0から1の間」となる指標として作られたものです。 ２種類考えてみました。 カテゴリ数標準化型と、情報量標準化型です。
なお、相互情報量係数は、 相互情報量 の発展版として、筆者が考えてみたものです。 既に、世の中に同じものがあれば、そちらに合わせますが、筆者の知る限りではないようなので、この名前にしています。
相互情報量を、カテゴリの少ない方の変数の、カテゴリの数の対数で割ります。 こうすることで、0から1の間になります。
この式を対数の法則で変形すると、結果的に、相互情報量の対数を、カテゴリの数に変形した定義式になります。
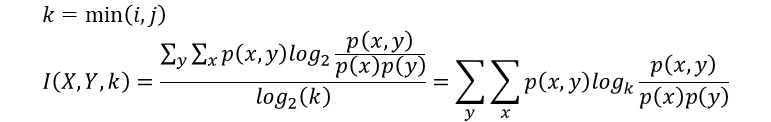
このあたりの考え方は、 平均情報量係数 と同じです。
相互情報量をそれぞれの情報量の平方根で割ります。
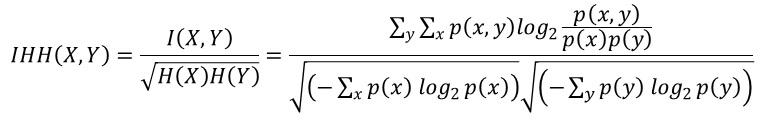
相互情報量は、２つの変数がまったく同じ時に最大値になり、片方の変数の情報量と同じになります。 この時、分母も片方の変数の情報量と同じになるため、１になります。
情報量標準化型相互情報量係数は、共分散と分散で相関係数を求める式と、同じ考え方をしています。
カテゴリ数標準化型は、２つの質的変数がまったく同じで、さらに、各カテゴリの頻度が同じ（等確率）の時に、最大値の１になります。
情報量標準化型は、２つの質的変数がまったく同じなら、最大値の１になります。 相関係数と似た振る舞いをするのは、情報量標準化型の方で、カテゴリ数標準化型は、相関係数よりも条件が厳しいです。
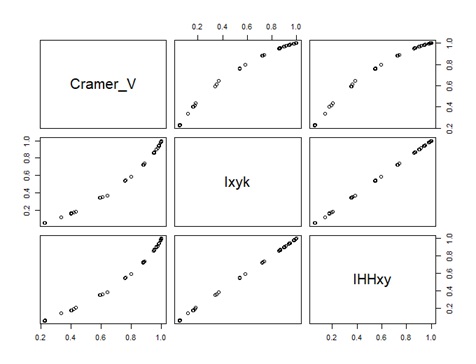
下図は、相関が高かったり、低かったりする13個の変数を適当に作って、計算した結果です。 Cramer_Vが クラメールの連関係数 、Ixykがカテゴリ数標準化型、IXXxyが情報量標準化型です。
カテゴリ数標準化型と、情報量標準化型は、完全に相関しています。相関係数は１です。
クラメールの連関係数は、0.5から0.9あたりは、相互情報量係数に比べて低めに出ています。
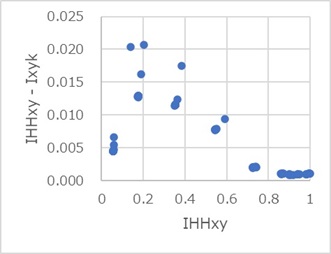
下図は、情報量標準化型IHHxyとカテゴリ数標準化型Ixykの差を縦軸にして、情報量標準化型を横軸にしたものです。
すべてプラス側なので、情報量標準化型の方が、常に大きいことがわかります。
相関係数のような感覚で、質的変数の類似度を分析するための尺度としては、相互情報量係数の方が良いと思います。
相互情報量 は、質的変数の場合の距離として使う使い方が適切のようです。
Rによる相互情報量 には、入力データの形式別で、相互情報量係数を求めるコードがあります。
Rによる相互情報量係数分析 には、変数が２個以上ある時に、すべての組合せについて相互情報量係数を求める方法があります。
「Natto 情報理論的アプローチによる探索的データ解析ツール」 鈴木了太 他 著
https://ef-prime.com/products/natto/doc/Suzuki_Nagai_and_Taniguchi_2006_revised_20070725.pdf
この論文では、０から１の間になる尺度として、相互情報量をXやYの平均情報量で割った尺度を紹介しています。
XやYの、片方の平均情報量で割った場合は、どちらで割るのかで値が異なります。
筆者の場合は、相互情報量と同じ対称性が相互情報量係数に欲しいので、情報量標準化型相互情報量係数には、XとYのそれぞれの平均情報量の平方根の積を使っています。
順路
次は
有向情報量分析
