Rによるデータ分析

Rによる相互情報量係数分析

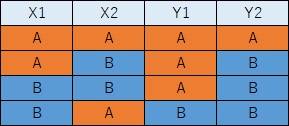
質的変数が複数あるテーブルデータについて、 相互情報量係数 と、 クラメールの連関係数 の両方の行列を作ります。

相互情報量係数分析

基本的に質的変数を扱う方法ですが、量的変数は １次元クラスタリング の方法で、質的変数に変換するコードが入っているので、 質的・量的が混合していたり、量的変数だけでも使えるようにしてあります。

library(vcd)
setwd("C:/Rtest")
Data <- read.csv("Data.csv", header=T)
Data1 <- Data # １次元クラスタリングの出力先を作る
n <- ncol(Data1)
for (i in 1:n) {
if (class(Data1[,i]) == "numeric") {
Data1[,i] <- droplevels(cut(Data1[,i], breaks = 3,include.lowest = TRUE))# ３分割する場合。量的データは、質的データに変換する。
}
}

CVMatrix <- matrix(0,nrow=n,ncol=n)
rownames(CVMatrix)<-colnames(Data1) # 行名をつける
colnames(CVMatrix)<-colnames(Data1) # 列名をつける
IxyMatrix <- CVMatrix
IxykMatrix <- CVMatrix
IHHxyMatrix <- CVMatrix

for (j1 in 1:n) {
for (j2 in 1:n) {
if(j1 >= j2){
TableXY <- table(Data1[,j1], Data1[,j2])# 分割表の作成
res <- assocstats(TableXY) # 連関分析
cramer_v <- res$cramer # クラメールの連関係数の抽出
CVMatrix[j1,j2] <- cramer_v # クラメールの連関係数の書き込み
CVMatrix[j2,j1] <- cramer_v # クラメールの連関係数の書き込み
Px <- TableXY
for (i in 1:nrow(TableXY)) {
Px[i,] <- sum(TableXY[i,])/sum(TableXY)
}
Hx <- 0
for (i in 1:nrow(TableXY)) {
Hx <- Hx + (-Px[i,] * log(Px[i,], 2))
}
Hx <- as.data.frame(Hx)[1,1]
Py <- TableXY
for (i in 1:ncol(TableXY)) {
Py[,i] <- sum(TableXY[,i])/sum(TableXY)
}
Hy <- 0
for (i in 1:ncol(TableXY)) {
Hy <- Hy + (-Py[,i] * log(Py[,i], 2))
}
Hy <- as.data.frame(Hy)[1,1]
Pxy <- TableXY/sum(TableXY)
pIxy <- Pxy*log(Pxy/Px/Py,2)
pIxy[is.na(pIxy)] <- 0
Ixy <- sum(pIxy)
k <- min(ncol(TableXY), nrow(TableXY))
Ixyk <- Ixy / log(k,2)
IHHxy <- Ixy / sqrt(Hx * Hy)
IxyMatrix[j1,j2] <- Ixy
IxyMatrix[j2,j1] <- Ixy
IxykMatrix[j1,j2] <- Ixyk
IxykMatrix[j2,j1] <- Ixyk
IHHxyMatrix[j1,j2] <- IHHxy
IHHxyMatrix[j2,j1] <- IHHxy
}
}
}
IxyMatrix# 相互情報量
CVMatrix # クラメールの連関係数
IxykMatrix# カテゴリ数標準化型相互情報量係数
IHHxyMatrix# 情報量標準化型相互情報量係数

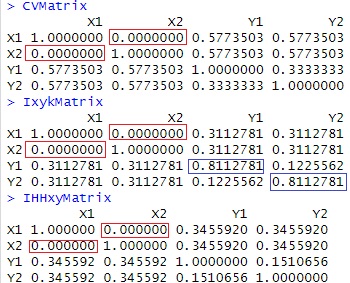
上から順に、クラメールの連関係数、カテゴリ数標準化型相互情報量係数、情報量標準化型相互情報量係数です。

X1とX2は、独立していますが、どの係数でも０になっています。

対角行列は、同じ変数同士で計算しています。 クラメールの連関係数と、情報量標準化型相互情報量係数は、必ず１になります。 カテゴリ数標準化型相互情報量係数は、等確率の場合は１ですが、等確率でないと、１よりも小さな値になります。

Rによるデータ分析