トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
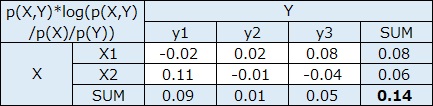
相互情報量と、 平均情報量 の関係は、共分散と分散の関係と似ています。
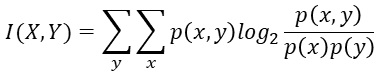
p(x)は、例えば、質的変数Xのカテゴリがx1、x2、x3なら、x1、x2、x3それぞれの発生数（頻度）をX全部の発生数で割った値です。 p(y)も同様です。
p(x,y)は、xとyのそれぞれの組合せについて、同様に求めた値です。
logの底は、2です。
平均情報量は、「情報量」というものがあって、情報量の期待値が平均情報量になっています。
式の形から考えると、「相互情報量（Mutual Information）」と呼ばれているものは、「平均相互情報量」でも良さそうに思うのですが、「相互情報量」と呼ぶのが一般的のようです。
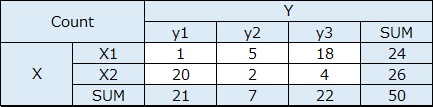
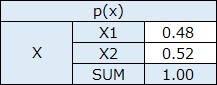
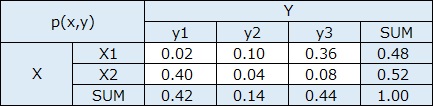
きちんと書かれている文献をまだ見たことがないのですが、相互情報量の最大値と最小値は、以下のようになるようです。 最小値は０です。 最大値は、カテゴリの数が少ない方の変数の、カテゴリの数の対数です。
頻度に偏りがない場合、logの計算の中身が１になるので、logの分が０になります。
偏っていると、０よりも大きな値になります。
正確な証明は、筆者は確認できていないのですが、相互情報量の最大値は、以下の式で求まるようです。
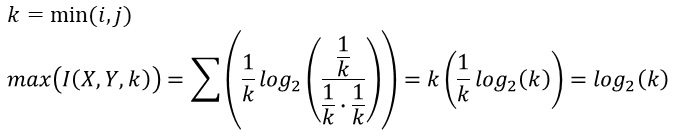
1行目は、i*jの分割表の時に、iとjの小さい方の値がkになります。
例えば、2*3の分割表なら、kは2で、相互情報量の最大値は、ちょうど1ということになります。 7*4の分割表なら、kは4で、相互情報量の最大値は、ちょうど2ということになります。
量的変数が複数ある時に、すべての変数の組合せについて、共分散を計算して、行列の形でまとめたものは、 「共分散行列」や「分散・共分散行列」と呼ばれます。
それと似た発想で、すべての質的変数の組合せについて、 相互情報量 を計算したものを、このサイトでは、「相互情報量行列」と呼んでいます。
共分散行列と相互情報量行列は似ています。
同じ変数について、共分散の計算をしても、その変数のみで分散を計算しても同じです。 そのため、共分散行列の対角成分は、の変数の分散になっています。
相互情報量行列の場合、対角成分は 平均情報量 と同じになっています。
これも、相互情報量と平均情報量の関係が、共分散と分散の関係と似ているため、このようになっています。
共分散を分散で標準化すると、相関行列になります。 相関行列は、対角成分がすべて１で、それ以外の成分は、相関係数になっています。
相互情報量行列を、平均情報量で標準化すると、対角成分がすべて１になり、それ以外の成分は、 正規化相互情報量 になっています。
上の例は、EXCELで作っています。 EXCELの関数で、底が2のlogを計算する場合は、log(X ,2)とします。Xのところに、変換したい値が入ります。
Rによる相互情報量 では、変数が２つあるデータをスタートにして、分割表を作ったり、量的変数を質的変数に変換するコードも入れています。
相互情報量をPythonで実装するので、アルゴリズムを教えてください。
相互情報量の意味とエントロピーとの関係 高校数学の美しい物語 2022
https://manabitimes.jp/math/1403#4
XとYが同じ分布の時に、相互情報量が最大値になることが説明されています。
順路
次は
正規化相互情報量
