です。
起こりにくい事象ほど、値が小さくなります。
平均情報量は、 情報量 の平均値です。
平均情報量は、「情報エントロピー」とも呼ばれます。 統計力学 のエントロピーと式の形が同じです。
平均情報量は、各事象の発生確率がPiの場合、
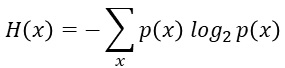
です。
起こりにくい事象ほど、値が小さくなります。
多様性の尺度として、平均情報量を使う場合は、
「平均情報量が大きい ＝ 多様」
という使い方をします。
対数には、「底（てい）」というものがあります。
対数は、様々な分野で使われますが、それぞれの分野によって、よく使われる底の数字が違います。 対数の底は、10にしたり、ネイピア数e（2.71828・・・）を使ったりします。
ソフトでも違っています。 EXCELのLOGという関数は、デフォルトが10になっていて、底を指定しないで使うと、10として計算されます。 Rのlogという関数では、デフォルトがネイピア数になっています。 例えば、EXCELや、Rで、底を３に指定したい場合は、log( X ,3)と書きます。 EXCELにLOG10、Rにlog10という関数があり、これらは底が10で固定です。 EXCELでは、LNという関数を使うと、底がネイピア数の対数を計算できます。
平均情報量は、いろいろな文献で出て来ますが、対数の底を書いていない文献がとても多いです。 書いてあるものには、「2」と書いてあるので、「2」が一般的な定義のようです。
データ分析をする時は、デフォルトで対数を使っても問題のないことが多いですが、平均情報量を自分で計算する時は、底を指定する必要があります。
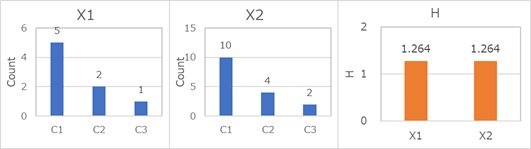
平均情報量は、頻度のばらつきが大きければ大きいほど、０に近くなります。
等確率、つまり、各カテゴリの頻度が同じ時に、最大値に近くなります。
正確な証明は、筆者は確認できていないのですが、平均情報量の最大値は、以下の式で求まるようです。
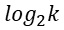
kというのはカテゴリの数です。 例えば、AとBというカテゴリしかない質的変数なら、kは2で、情報量の最大値は、ちょうど1ということになります。 カテゴリの数が4なら、kは4で、情報量の最大値は、ちょうど2です。
平均情報量は、 質的変数のばらつきの尺度 になります。
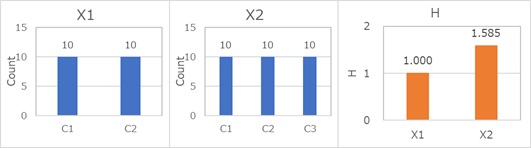
平均情報量は、頻度のばらつきの大きさと、カテゴリの数の両方で決まります。
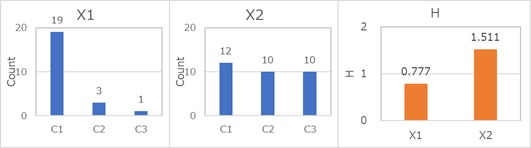
分散や標準偏差は、「ばらつきが大きいほど、大きい」という尺度なので、一見すると、逆のように見えます。
一方、「頻度のばらつきが大きい」というのは、ひとつのカテゴリに偏っているということなので、 「頻度のばらつきが小さい方が、まんべんなくばらついている」という見方もできます。 分散や標準偏差とは、後者の方の考え方をすると、値の出方が合っています。
「情報量」 biopapyrus
https://bi.biopapyrus.jp/seq/entropy.html
情報エントロピーの取り得る範囲が、０から、カテゴリの数の対数の間になることが示されています。
順路
次は
平均情報量係数
