「質的変数には、ばらつきの尺度はあるのか？」、「そもそも質的変数のばらつきとは、どういうものか？」というのが、このページの話です。
カイ二乗値は、カイ二乗検定で使われる尺度です。
カイ二乗検定は、質的変数が１つあって、その質的変数のばらつき（頻度のばらつき）を調べる時には、「適合度の検定」と呼ばれます。 質的変数が２つある場合は、「独立性の検定」と呼ばれます。
カイ二乗値は、各カテゴリの頻度が同じ（等確率）の場合、０になります。
頻度のばらつきが大きいと、大きな値になります。
平均情報量 は、各カテゴリの頻度が同じ（等確率）場合、最大値になります。 頻度のばらつきが大きいと、０に近くなります。
平均情報量係数 は０から１の数字になります。
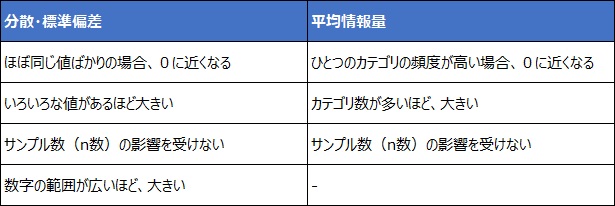
分散や標準偏差には、以下のような特徴があります。
このように考えると、質的変数の場合で、分散や標準偏差と似た性質を持っているのは、 平均情報量 と考えられます。
質的変数には、値の大きさがないため、「数字の範囲が広いほど、大きい」だけが当てはまらないですが、それ以外は、以下のように対応します。
平均情報量係数 は、 平均情報量 を、カテゴリの数の違いは出ないように標準化した尺度になります。
順路
次は
歪度と尖度
