左から順に、元データの構造、相互情報量分析、有向情報量分析です。 元の構造と違うのは、Y1とY2の間に線が引かれていることです。 有向情報量分析では、疑似相関を見破る仕組みがないので、Y1とY2が結ばれます。
有向情報量分析は、質的変数同士の関係について、非対称な構造を見つけるための方法の一種です。 有向グラフになるデータの構造 （ 情報量の変化があるデータの構造 ） のひとつとして、 定量的な仮説の探索 に使えます。
有向情報量分析は、 相互情報量 の発展版として、筆者が考えてみたものです。 既に、世の中に同じものがあれば、そちらに合わせますが、筆者の知る限りではないようなので、この名前にしています。
２つの変数があった時に、それらには平均情報量の違いがあります。
有向情報量分析では、この違いに対して矢印を引くのですが、平均情報量だけでは、単に平均情報量の値が違うだけなのか、何らかの関係があることで、その差が生まれているのかが区別できません。
そこで、相互情報量を事前に確認して、相互情報量が高い場合についてだけ、平均情報量の差に着目するようにします。
相互情報量の代わりに、 相互情報量係数 、 平均情報量の代わりに、 平均情報量係数 を使うこともできます。
係数の方を最大値が１で固定されるので目安としては使いやすいですが、 実務上、相互情報量も平均情報量は、２より大きくなることはあまりないので、どちらを使っても大差はないようです。
有向情報量分析では、「２つの変数に関係がある」と「２つの変数には平均情報量に差がある」の２つについて、しきい値を超えるかどうかで判断します。
このサイトでは、筆者の経験を元に、前者を0.1、後者を0.0001にしています。
このしきい値について、統計的な厳密性を考えるのなら、検定のアプローチに進んでも良いかもしれません。
有向情報量分析では、平均情報量が高い方から低い方に向かって、矢印を書くようにしています。
平均情報量の高さの違いと、実際のデータの関係については、 平均情報量 のページに例があります。
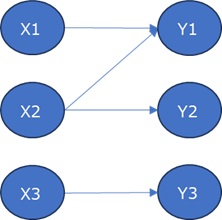
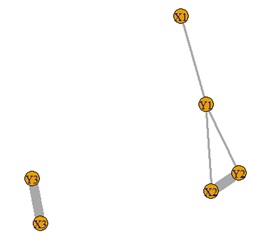
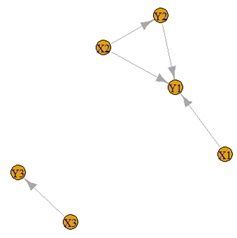
左から順に、元データの構造、相互情報量分析、有向情報量分析です。
元の構造と違うのは、Y1とY2の間に線が引かれていることです。
有向情報量分析では、疑似相関を見破る仕組みがないので、Y1とY2が結ばれます。
Rによる有向情報量分析 があります。
R-EDA1
で、簡単にできます。
順路
次は
相互情報量行列
