 Rによるデータ分析
Rによるデータ分析
 Rによるデータ分析
Rによるデータ分析
連関係数 を計算して、相関の大きいものだけをネットワークグラフで抽出する方法です。
変数の類似度の分析 です。
相関係数 のように、量的変数の類似度の分析では、線形の関係しか見ていませんが、 質的変数の類似度の分析をベースにした方法を使うと、量的変数の非線形の関係も見ることができるようになります。 数値の情報が粗くなる弱点はありますが、探索的データ分析では、あまり気にしなくて良いと思います。
基本的に質的変数を扱う方法ですが、量的変数は 1次元クラスタリング の方法で、質的変数に変換するコードが入っているので、 質的・量的が混合していたり、量的変数だけでも使えるようにしてあります。
library(igraph) #ライブラリを読み込み
library(vcd) #ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- Data # 1次元クラスタリングの出力先を作る
n <- ncol(Data1) # データの列数を数える
for (i in 1:n) { # ループの始まり。データの列数を数えて同じ回数繰り返す
if (class(Data1[,i]) == "numeric") { # 条件分岐の始まり
Data1[,i] <- droplevels(cut(Data1[,i], breaks = 5,include.lowest = TRUE))# 5分割する場合。量的データは、質的データに変換する。
} # if文の処理の終わり
} # ループの終わり
GM2 <- matrix(0,nrow=n,ncol=n) # 出力先を作る
for (i in 1:(n-1)) { # ループの始まり
for (j in (i+1):n) { # ループの始まり
cross<-xtabs(~Data1[,i]+Data1[,j],data=Data1)# 分割表の作成
res<-assocstats(cross)# 連関分析
cramer_v<-res$cramer# クラメールの連関係数の抽出
GM2[i,j] <- cramer_v# クラメールの連関係数の書き込み
GM2[j,i] <- cramer_v# クラメールの連関係数の書き込み
} # ループの終わり
} # ループの終わり
rownames(GM2)<-colnames(Data1) # 行名をつける
colnames(GM2)<-colnames(Data1) # 列名をつける
GM2[GM2<0.8] <- 0 # 相関係数の絶対値が0.8未満の場合は0にする(非表示にするため)
GM3 <- GM2*10 # 一番大きな値が10になるように修正(パスの太さを指定するため)
GM4 <- graph.adjacency(GM3,weighted=T, mode = "undirected") # グラフ用のデータを作成
plot(GM4, edge.width=E(GM4)$weight) # グラフを作成

以下は、 偏連関係数 の性質を調べた時に使ったものです。
library(vcd) #ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- Data # 1次元クラスタリングの出力先を作る
n <- ncol(Data1) # データの列数を数える
for (i in 1:n) { # ループの始まり。データの列数を数えて同じ回数繰り返す
if (class(Data1[,i]) == "numeric") { # 条件分岐の始まり
Data1[,i] <- droplevels(cut(Data1[,i], breaks = 3,include.lowest = TRUE))# 3分割する場合。量的データは、質的データに変換する。
} # if文の処理の終わり
} # ループの終わり
asso <- matrix(1,nrow=n,ncol=n) # 出力先を作る
for (i in 1:(n-1)) { # ループの始まり
for (j in (i+1):n) { # ループの始まり
cross<-xtabs(~Data1[,i]+Data1[,j],data=Data1)# 分割表の作成
res<-assocstats(cross)# 連関分析
cramer_v<-res$cramer# クラメールの連関係数の抽出
asso[i,j] <- cramer_v# クラメールの連関係数の書き込み
asso[j,i] <- cramer_v# クラメールの連関係数の書き込み
}
}
rownames(asso)<-colnames(Data1)
colnames(asso)<-colnames(Data1)
solveasso <- solve(asso)
passo <- solveasso
for (i in 1:n) {
for (j in 1:n) {
if(i >= j){
passo[i,j] <- -solveasso[i,j] / sqrt(solveasso[i,i] * solveasso[j,j])
passo[j,i] <- passo[i,j]
}
}
}
rownames(passo)<-colnames(Data1)
colnames(passo)<-colnames(Data1)
asso2 <- asso^2
passo2 <- passo^2
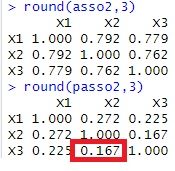
round(asso2,3)# 連関係数行列
round(passo2,3)# 偏連関係数行列
祐子 武田 氏の記事
質的変数の総当たりの組み合わせから、連関係数を求める方法は、このページを参考にさせていただきました。
https://qiita.com/ytakeda/items/058e83ebdd721f87ceb4

