カテゴリの分解分析

分解分析の方法としては、主成分分析、因子分析、独立成分分析があり、データを新しい変数のグループに変換します。分解分析のページに入っていませんが、コレスポンデンス分析も、これらと似た方法です。

ところで、分解分析のページでは量的変数の方法として、主成分分析、因子分析、独立成分分析を使っていますが、ダミー変換すると、これらは質的変数の場合にも使えます。質的変数に変換すると、カテゴリの類似度の分析の一種になります。コレスポンデンス分析も同様です。

このサイトでは、このような方法を「カテゴリの分解分析」と呼ぶことにしています。

カテゴリの分解分析の特徴

カテゴリの類似度の分析の分析には、いくつか種類がありますが、「グループ分け」という機能がないです。「塊ができる」というところから、人が判断する必要があります。

カテゴリの分解分析では、成分を求めるので、それが要約を表すようになっています。

コレスポンデンス分析の一般的な使い方では、データを新しい変数のグループに変換します。そして、新しい変数のグループとして作ったデータを、座標データとして扱い、カテゴリの近さを距離の尺度で調べます。

分解分析として使う時は、カテゴリ同士の距離ではなく、ダミー変換した変数との相関を見て行きます。

ICA
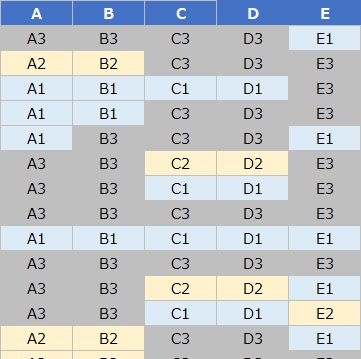
このページでは、上のようなデータを例にしています。 A、B、C、D、Eという５個の変数があります。サンプル数は1000です。それぞれ、1、2、3、という３個のカテゴリがあります。

このデータについて、ダミー変換して独立成分分析をすると、下のようになります。
ICA ICA

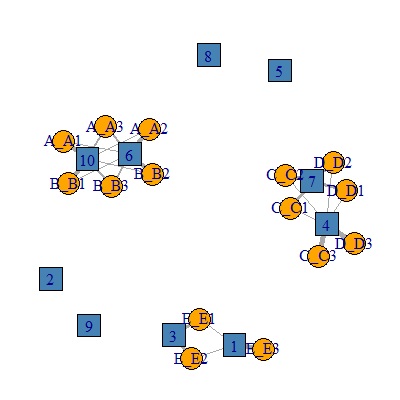
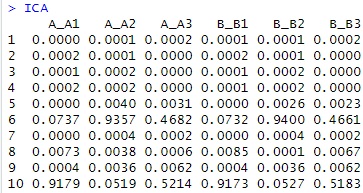
まず、３つのグループがあり、AとB、CとD、Eと分かれています。また、数字をよく見ると、A1とB1、A2とB2、A3とB3といった組合せは、数字が似ていることもわかります。

このようにして、カテゴリが分類できます。

上のグラフで、Aの数字をよく見ると、A1は10に寄っていて、A2は6に寄っていて、A3は10と6に半々くらいになっています。このようにして、成分の数はカテゴリの数よりも１つ少なくなり、ひとつのカテゴリは、複数の成分に分散する形になります。

変数ごとにひとつのカテゴリを除いたのが、下のグラフす。ごちゃごちゃした感じが、少し改善します。
ICA

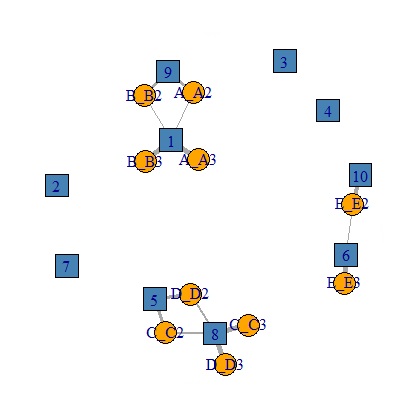
方法には以下のような違いがあります。結論としては、独立成分分析が一番、使い勝手が良いようです。

独立成分分析では、ひとつのカテゴリを除いて、ひとつのカテゴリに対して、主成分が１つ対応する結果になりやすいです。

コレスポンデンス分析は、独立成分分析よりも思ったような結果になりにくいです。下の例では、AとB、CとDという２つのグループが完全に分離できていないです。
ICA

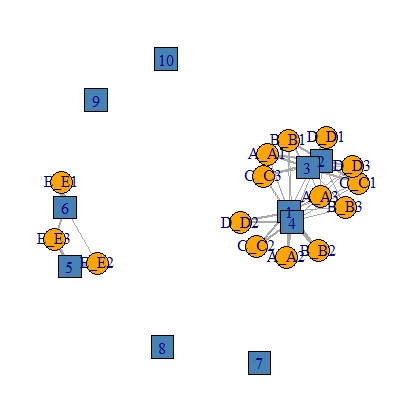
独立成分分析では、ひとつカテゴリだけは、複数の主成分に分散して対応する形になってごちゃごちゃになるのを避けるために、質的変数ひとつにつき、ひとつのカテゴリを分析から外す対策があります。

コレスポンデンス分析では、この対策をすると、手法が想定しているデータでなくなるため、エラーになります。

主成分分析では、ひとつのカテゴリに対して、主成分が１つ対応するようなカテゴリができにくく、主成分とカテゴリが多対多の関係になります。コレスポンデンス分析よりも、さらに精度が悪いです。
ICA

そのため、結果の解釈が難しいです。

因子分析は、コレスポンデンス分析や主成分分析よりは、精度が良いです。ただ、Eのカテゴリは２つしかないのに、６個の成分が結び付いています。独立成分分析と違って、「不要な成分は使わない」という結果になりにくいです。
ICA

また、因子分析では、「質的変数ひとつにつき、ひとつのカテゴリを分析から外す対策」の方法のみです。外さないと、エラーになります。