要約分析と分解分析の違い というページがあります。 このページは、分解分析の中の、 独立成分分析 、 因子分析 の違いについて、調べたものです。 また、 主成分分析 も参考として入っています。
これらは計算方法が違いますが、 EDA（探索的データ分析） や、説明変数の代わりとして使う場合は、同じ使い方をします。
要約分析と分解分析の違い という考え方をするのなら、主成分分析は要約分析の方法ではないですが、 要約分析と分解分析では、結果がほぼ同じになることがありますし、 因子分析や独立成分分析は、計算がうまくできないことがあるため、主成分分析は分解分析の代用として使えることがあります。
元の変数の特徴を際立たせるような形で、要約変数を作るのは、因子分析か独立成分分析というのが、下記からわかることでした。 現実のデータで、きれいな正規分布のことは少ないので、それも加味すれば、まず、最初に試すのは独立成分分析が良さそうです。
なお、因子分析と独立成分分析は、先に主成分分析をして、抽出する変数の数の検討をしないとエラーになりやすいです。 その意味では、一番手軽なのは主成分分析です。
機械的に、精度の高いモデルを作るのなら、主成分分析をベースとした主成分回帰分析がベストです。
X01のグループと、X02のグループを区別できるのは、因子分析だけです。
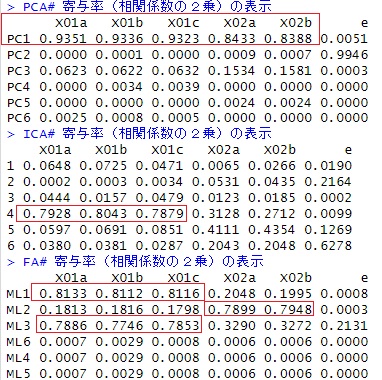
X01と、X02を区別できるのは、独立成分分析だけです。
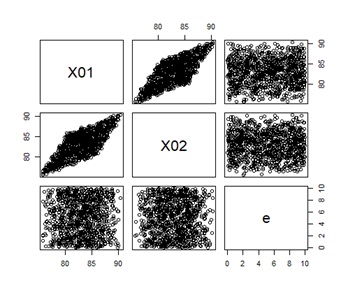
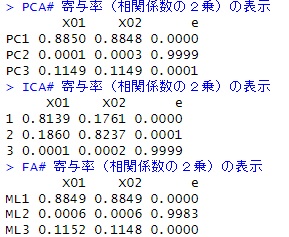
X01と、X02を区別できるのは、独立成分分析だけです。
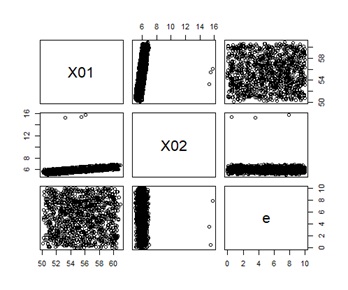
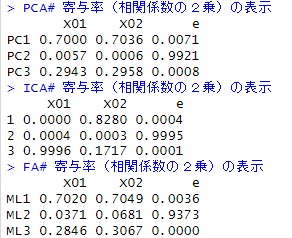
X01と、X02を区別できるのは、独立成分分析だけです。
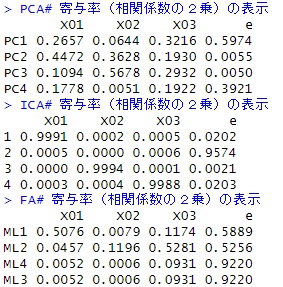
主成分回帰分析 や 隠れ変数の探索 では、説明変数の前処理として、主成分分析、独立成分分析、因子分析等のバリエーションがあります。
前処理の方法が変わると、考察できることが変わります。
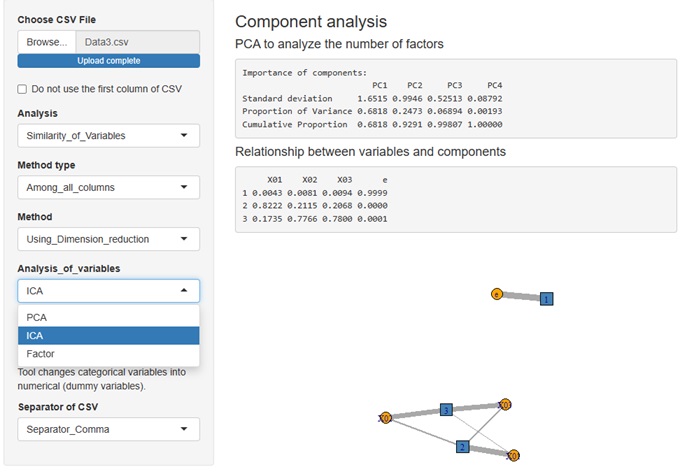
Rによる分解分析 では、主成分分析、独立成分分析、因子分析で求める各要約変数の寄与率だけを比較する分析の実施例があります。
R-EDA1
では、３つの手法を選べます。
順路
次は
SEM・共分散構造分析
