トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

SEM・共分散構造分析

「SEM（Structural Equation Modeling　：　構造方程式モデリング）」と「共分散構造分析」は、同じものです。

「共分散構造分析」の方が、文献は多いようです。 また、筆者の場合は、「SEM」と言えば、電子顕微鏡のSEM（Scanning Electron Microscope）の方が馴染みがあって、 ややこしくなります。 そんな事もありますので、以下では「共分散構造分析」にしています。

共分散構造分析は、簡単に言えば、 潜在変数 も扱える パス解析 です。

パス図と構造方程式

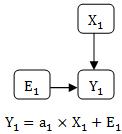図は、XとYがひとつずつで、「YをXで表す」という事を表現したものです。 XとYが比例関係にあるデータのパス図と構造方程式はこうなります。

YとXの数が増えても 同じような要領で、各変数の関係を、 線形和 で式にします。

共分散構造分析のソフトは、パス図を描けば、構造方程式はソフトが自動で作ってくれるものが一般的なようです。

誤差の扱い方

パス図を描く時に、「E」や「e」というものを変数につなげるようにするのですが、これが誤差（Error　：　エラー）を表します。 実際のデータには誤差があるので、「E」がないと、式とデータが合わなくなります。

筆者自身は、構造方程式の中で、この「E」の意味がなかなかわかりませんでした。

構造方程式の形を見ると、誤差は、 回帰分析 や「定数（Y切片）」と呼ばれているものと同じように見えますが、役割が違います。 「定数」として扱うと、実際のXやYのデータの関係を表す事ができないです。 Eは、YとXの値の組み合わせによって、一緒に変わっている値です。

ちなみに、統計学的に正確な記述を意識している本では、 回帰分析のモデル式に誤差項を書いています。

共分散構造分析の進め方

共分散構造分析とは、図の例で言えば「a」の値（係数）を推定していく事が解析の目的になっています。

YとXが増えると、構造方程式は、何行もある式の集まりになりますが、これは連立方程式の形をしています。 そのため、係数の推定とは、連立方程式を解くイメージと同じです。

ただ、構造方程式の場合は、誤差の項があるので、統計的な解き方をします。

また、構造方程式とデータだけでは、係数がひとつの値として推定できない事がありますので、 式に制約条件を加える事が必要になる事もあります。 （潜在変数を入れる場合は、条件の付け方がけっこう大変です。）

共分散構造分析の強みと弱み

共分散構造分析は、 パス解析 や 因子分析 と同じ事ができ、さらにいろいろなモデルも扱えるようになっているものです。

ただ、モデルの自由度が高い分、解析者が自分で設定しなければいけない所が多く、なかなか扱いにくい手法でもあります。 （扱いに慣れれば、解決する問題かもしれませんが、、、）

共分散構造分析の潜在変数と、因子分析の潜在変数の違い

潜在変数は、元のデータには含まれていない変数です。

因子分析では、
「潜在変数　＝　因子]
となっています。

一方、共分散構造分析では、元のデータには含まれていない変数として使われていて、 因子分析の意味での使い方は、そのひとつになっています。 もうひとつは、因子ではなく、結果を要約した変数という意味での使い方です。 つまり、共分散構造分析には、
「潜在変数　＝　因子」
と、
「潜在変数　＝　結果を要約した変数」
の２つの使い方があります。 「結果を要約した変数」の例は、 主成分分析 で出て来る主成分です。

ややこしくなりますが、共分散構造分析では、ある変数のグループについて、因子になっている潜在変数が、 別の変数のグループからは結果を要約した変数になっているモデルを作ることもできます。

LiNGAM的な方法

LiNGAM は、パス解析の、パス図を作る手順のところを、自動でやってしまう方法として使うことができます。

共分散構造分析は、パス解析に潜在変数も入っているパス図を作ります。 筆者の知る限りでは、共分散構造分析のパス図も作ってしまうLiNGAM的な方法は、世の中にはないようです。

ばらつきの作り方

参考文献

「図解でわかる共分散構造分析　データから「真の原因」を探り出す新しい統計分析ツール」　涌井良幸、涌井貞美　著　日本実業出版社　2003
共分散構造分析の特徴や使い方を、まず、検証的因子分析モデルで解説しています。 その後で、共分散構造分析は、検証的因子分析モデル以外にも使える事を解説しています。
変数の関係を視覚的に、かつ簡単に描く方法としてパス図を紹介しています。 しかし、パス図だけでは「絵に描いた餅」なので、定量的な解析にするための方法として、共分散構造分析を紹介しています。
ソフトは、AMOSを使っています。
平均値の構造も含めた場合は、「平均・共分散構造分析」と呼んでいます。

「Excelで学ぶ共分散構造分析とグラフィカルモデリング　Excel2013/2010/2007対応版」 小島隆矢・山本将史　著　オーム社　2013
SEMと共分散構造分析は、同じ手法に対して、呼び方が違う事を説明しています。 現在は、平均値の構造も含まれるので、「共分散構造分析」は手法の内容と合っていない、としています。
この本は、ソフトも用意して、ネットからダウンロードできるようになってています。

「入門共分散構造分析の実際」 朝野煕彦、鈴木督久、小島隆矢　著　講談社　2005
実際に分析する時の疑問にも答える形になっています。

「共分散構造分析 : 構造方程式モデリング　技術編」 豊田秀樹　編著　朝倉書店　2003
共分散構造分析では、モデルを考えて、モデルの妥当性をデータを使って検証する進め方が普通です。
一方で、「分析者の考えたモデルは最良と言えるのかを知りたい。」、 「他にはモデルを考えられないのか？」、というニーズもあるそうです。 探索的にモデルを作る方法として、 遺伝的アルゴリズム（GA） を使う試みが紹介されています。
ちなみに、この本は「技術編」ですが、「数理編」や「疑問編」などもあり、このシリーズはかなり充実しています。

順路 次は 独立成分分析