主成分分析における、相関行列と共分散行列の違い のページでは、共分散行列を使う場合の話がありますが、このページは、相関行列を使う場合だけです。
下のデータを例にします。
A、B、C、Dとなっている変数では、その変数同士で、相関が高く、散布図にするとプロットが直線状に並んでいます。
A、B、C、D、Eのグループ間では、相関がまったくありません。
上のデータを主成分分析した結果が、下になります。
各主成分と相関が高ければ、線で結ばれるようになっています。
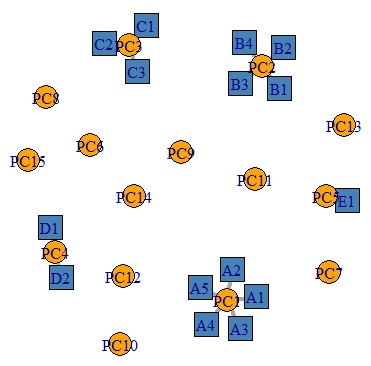
各グループが、それぞれ１つの主成分と結び付いています。
５つのグループが、５つの主成分で表現できるようになります。 元は、15変数あったのが、５変数に要約できました。
下のデータでは、７つの変数がありますが、それぞれの間にまったく相関がありません。
上のデータを主成分分析すると、下のグラフになります。
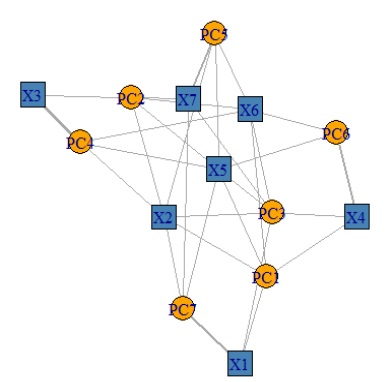
元の変数と、主成分が、多対多の関係になっています。
要約できない場合は、元の変数１個について、主成分が１個対応するような結果の方が、使い勝手が良いのですが、そうはならないです。
上記のように、主成分分析には、要約の機能があります。 実務のデータでは、変数同士に高い相関があることがあり、それが、考察を難しくするため、要約の機能は役に立ちます。
一方、要約できない場合に、変数１個と主成分１個が対応せず、多対多の関係になってしまうのは、扱いにくい性質です。
因果関係の分析では、１対１になってくれると考察がしやすいです。 １対１にする方法としては、 因子分析 や 独立成分分析 があります。
ただし、 因子分析 や 独立成分分析 でも、１対１にはならない場合があったり、 因子分析 にはエラーが出やすい特徴があります。 そのため、これらの３つの方法は、場合によって使い分けると良いようです。 （分解分析の違い）
主成分分析の直接的な改善としては、 しきい値主成分分析 があります。
「図解でわかる多変量解析」 涌井良幸・涌井貞美 著 日本実業出版社 2001
相関行列を使う時と、共分散行列を使う時の違い多、絵も豊富に使いながら、丁寧に解説されています。
順路
次は
主成分分析のルート
