主成分分析における、相関行列と共分散行列の違い

主成分分析のソフトでは、相関行列を使うか、共分散行列を使うかを使い分ける必要があります。
PCA
例えば、Rで主成分分析をする時のコードが上ですが、「scale = TRUE」と書くと、相関行列を使います。「scale = FALSE」と書くと、共分散行列になります。

データを標準化してから、共分散行列を計算したものは、相関行列と同じです。相関行列を使うということは、標準化したデータで、主成分分析をすることになります。

共分散行列を使う場合

PCA PCA
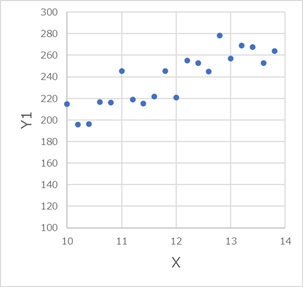
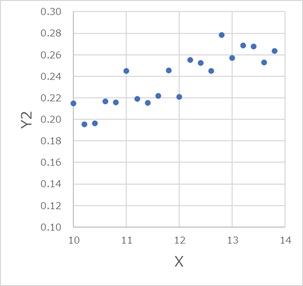
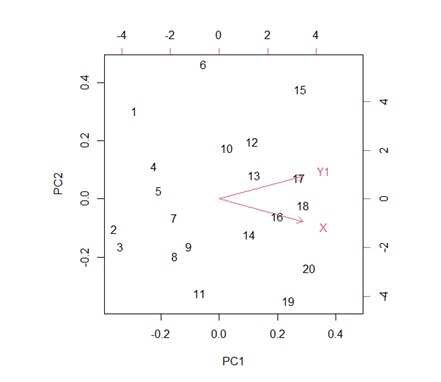
上の２つのグラフは、X、Y1、Y2という３種類の変数があります。 XとY1、XとY2、という２つの組合せについて、共分散行列を使った主成分分析をしてみます。

２つのグラフは、見た目がとても似ています。Y2の1000倍がY1になっていて、それ以外の違いはないです。

共分散行列を使った主成分分析の結果が、下のグラフです。グラフの中の数字は、元のデータの位置を、番号で表しています。横軸のPC1は第１主成分、縦軸のPC2は第２主成分です。
PCA PCA

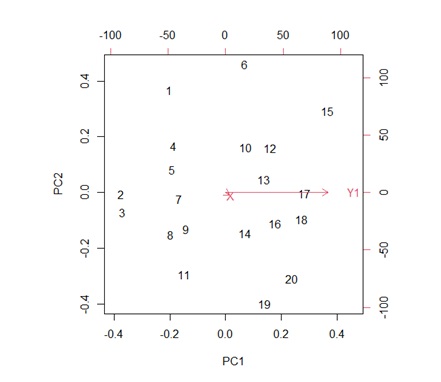
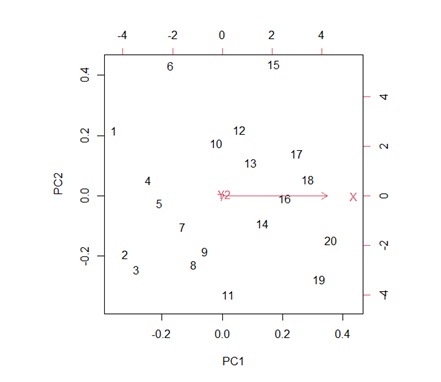
左のグラフでは、第１主成分とY1が同じ方向になっています。 Xは、どちらの方向を向いているのかわからないくらい、矢印が短いです。これは、Y1だけで、データのばらつき方のほとんどが説明できてしまうことを示しています。

右のグラフでは、第１主成分とXが同じ方向になっています。 Y2は、どちらの方向を向いているのかわからないくらい、矢印が短いです。これは、Xだけで、データのばらつき方のほとんどが説明できてしまうことを示しています。

このように、共分散行列を使った主成分分析では、元のデータの数字の大きさで、第１主成分が決まって来ます。

上の２つのケースについて、相関行列を使った主成分分析をした場合の結果が下のグラフになります。
PCA PCA

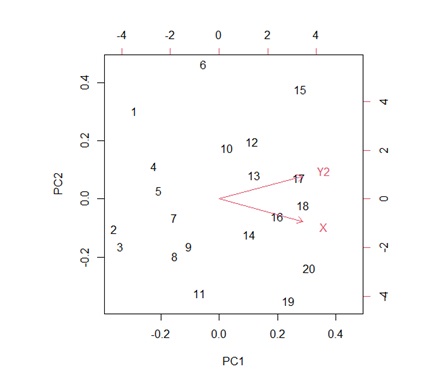
結果は、まったく同じになります。これは、標準化すると、Y1とY2の違いがなくなるためです。

第１主成分は、２つの矢印の中間を通るにようにして決まっています。

Rでは、TRUEかFALSEかで使い分けられますが、 R-EDA1 では、相関行列を使う方しか、使えるようになっていません。

筆者の場合は、単位の異なる変数が混ざったデータを分析することが普通なので、共分散行列を使う主成分分析が必要になったことがないです。

お金のデータなどで、数字の大きい変数が主成分として大きく出るような分析をしたいのなら、共分散行列を使う方を使った良いかもしれません。

「図解でわかる多変量解析」涌井良幸・涌井貞美著　日本実業出版社　2001
相関行列を使う時と、共分散行列を使う時の違い多、絵も豊富に使いながら、丁寧に解説されています。