トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

主成分分析のルート

主成分分析 は、「共分散行列（相関行列）を求めます。次に、固有値分析をします。」という手順が、よく知られています。

この手順は、ルートの内のひとつです。

主成分分析の中の内積

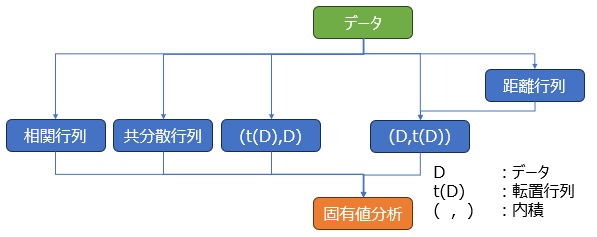
主成分分析では、上記のように、共分散行列や相関行列を固有値解析することで主成分を求めていきます。

共分散行列や相関行列は、すべての変数の組合せについて、１つずつ共分散や相関係数を求めて、それを行列形式にまとめて作る手順がイメージしやすいです。

一方、テーブルデータを行列として、その行列と、転置行列の内積(t(D),D)を求めることでも、共分散行列や相関行列を求めることができます。 詳しい説明は、 相関行列と内積 にあります。

もうひとつの内積による主成分分析

内積の計算は、(D,t(D))というようにして求めるものもあります。 (t(D),D)では、変数の数（列数）の正方行列ができますが、(D,t(D))では、サンプルの数（行数）の正方行列ができます。

固有値分析 に詳しい説明がありますが、 面白いことに、(t(D),D)と(D,t(D))のそれぞれについて、固有値分析をすると、求まる主成分は同じです。 つまり、どちらのルートでも、主成分分析になります。

距離行列からの主成分分析

多次元尺度構成法 にあるように、距離行列は、(D,t(D))の形の、内積に変換できます。 そのため、距離行列からスタートすると、途中から内積に持ち込むことができます。

つまり、テーブルデータからスタートした場合、直接内積(D,t(D))に進むことができますが、 テーブルデータを、ユークリッド距離の距離行列に変換してからでも、同じ結果を出すことができます。

テーブルデータがスタートの場合、距離行列を経由しなくても、内積に進むことができるので、普通の主成分分析をするだけなら、 使うことのない知識ですが、 非線形のための主成分分析 をしたい時には、アプローチのひとつになるので、役に立つ知識です。

順路 次は 非線形のための主成分分析