トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

EDA（探索的データ分析）

EDAは、「Exploratory Data Analysis：探索的データ分析」の略です。

一般的なEDA

「EDA」という言葉は、1990年代頃には、すでに使われています。「 回帰 や ラベル分類 のモデルを作って、予測」、という事をする前に、モデルを作るためのデータを、よく調べる作業として紹介されています。 よく調べることで、モデルの妥当性や精度を確保します。

EDAの作業として説明されるものは、以下のようなものです。

このサイトのEDA

世の中の課題に対して、実際に予測モデルを作っていく時のEDA（探索的データ分析）では、上記のようなものでは足りないです。 もっといろいろなデータ分析をします。

話を広げて、ここで、予測モデルを作る目的での、EDA（探索的データ分析）をいったん離れて、「EDA（探索的データ分析）」とは、どういうものかを考えます。

まず、「 データマイニング 」と呼ばれているものは、探索的なデータ分析をして、データから役に立つ情報を見つけようとする（マイニングする・掘り当てる）方法です。

また、「因果探索」などとも呼ばれますが、 定量的な仮説の探索 でしているデータ分析は、探索的なデータ分析です。

予測モデルを作る時のEDAと、データマイニングや因果探索が共通している点は、表形式になっているデータ（表データ、テーブルデータ）を、探索的に調べる点です このサイトでは、その視点でEDAをまとめることにしています。

データマイニングとEDA

2000年前後に流行っていた「データマイニング」では、 「データマイニング」の名前の通りに、データから役に立つ情報を見つけることを目的とした分析が盛んに行われていたようです。

その一方で、データマイニングに使っているモデルを、予測モデルとして使う研究もありました。 こちらの研究については、その10年後くらいから「機械学習」と呼ばれるのが一般的になっています。

ややこしい話になるのですが、当時、データマイニングの分野で「EDA」と呼ばれていたものは、予測モデルを構築する前の事前分析を指していたようです。 言葉そのものから考えると、「データマイニング　≒　EDA」と考えたいところですが、当時、「EDA」という言葉を使う人の認識は違っていたようです。

このサイトのEDAの体系

データ分析の手法の分類としては、「教師あり・教師なし」、「線形・非線形」、「目的変数が、量的・質的」、「説明変数が、量的・質的」といったものがあります。

このサイトでは、表形式のデータへのEDAのアプローチとして、大きく７種類に分けました。


下記は、各アプローチの紹介です。例はすべて、40行、10列（40サンプル、10変数）になっている表データを使っています。
EDA

基本分析

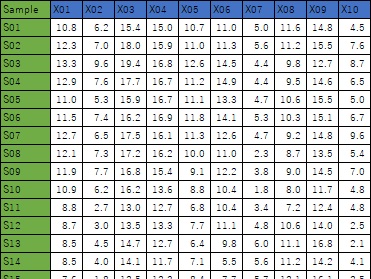
変数ごとの統計量や、データの数を見るのは基本になります。

また、表の全部は難しいかもしれませんが、最初と最後の５行ずつ、などについて、生のデータを見て、データの桁の数などを確認します。
EDA

変数の類似度の分析

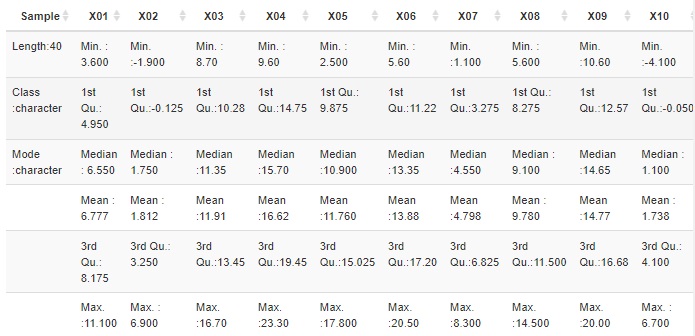
変数の類似度の分析 は、表の列の項目同士の関係に注目します。

「X01とは、X02、X03、X04 が似ている」といったことがわかります。 「平均値が近い」、「相関が高い」など、似ていることの判断基準で結果が変わります。
EDA　 EDA

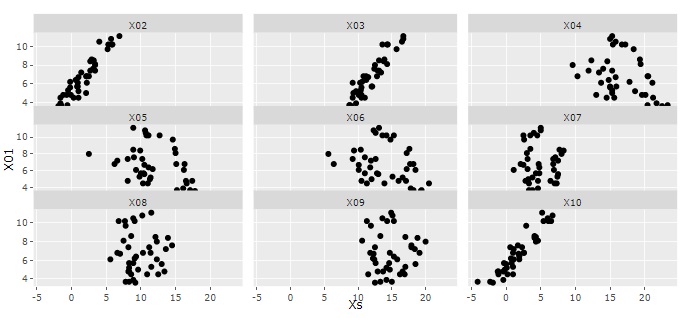
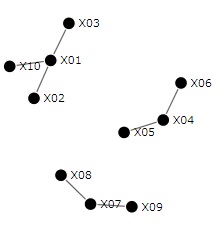
総当たりで、２つずつの変数の組合せについて、 ２次元散布図 を見る方法が基本になります。

上記で、EDAは、「 回帰 や ラベル分類 のモデルを作る前の作業」、と説明しているので、ややこしくなるのですが、 回帰 や ラベル分類 の手法は、EDAの手法の一種として使うことができます。 EDAの手法の一種としては、変数の関係を調べる方法の一種になります。

サンプルの類似度の分析

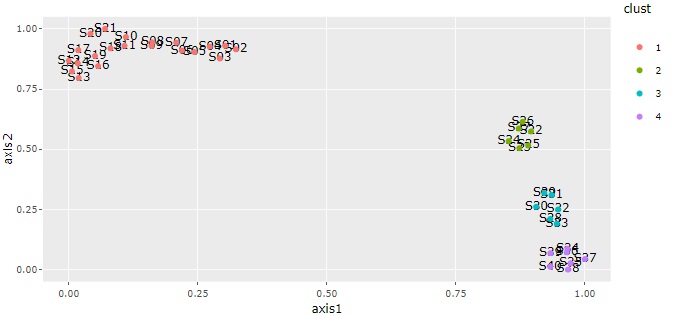
サンプルの類似度の分析 では、表の行の項目同士の関係に注目します。 変数のや組合せ方で、結果が変わります。

クラスター分析 が代表的です。

Sで始まる項目の類似度がわかります。
EDA

カテゴリの類似度の分析

カテゴリの類似度の分析 は、質的変数の中にあるカテゴリの関係に注目します。 表の行や列の項目は、それほど重視しません。

質的変数のデータで使われることの多い方法です。 アソシエーション分析 が代表的です。

質的変数を ダミー変換 すると、 変数の類似度の分析 の方法も、この分析に使えます。

量的変数を １次元クラスタリング すると、 カテゴリの類似度の分析 の見方で、量的変数のデータを分析することもできます。 下の例は、「各変数とその区間」というカテゴリになっています。
EDA

多対多の分析

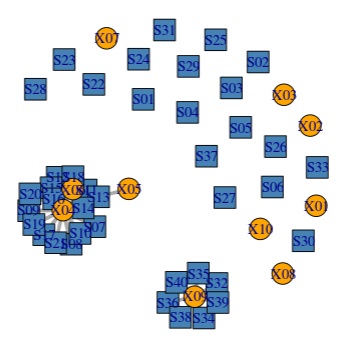
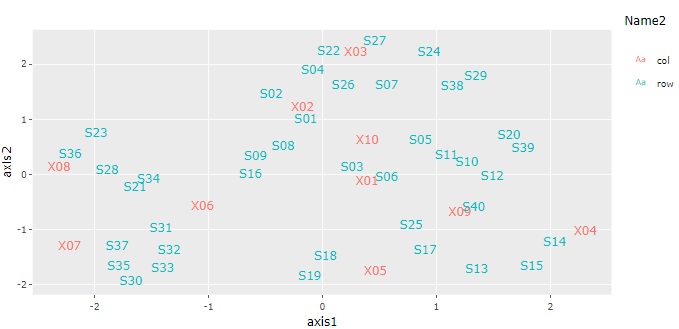
多対多の分析 は、表の行の項目と、列の項目の関係に注目します。

発生回数（頻度）のデータで使われることの多い方法です。 ２部グラフ や コレスポンデンス分析 が代表的です。

このアプローチから、 変数の類似度の分析や、サンプルの類似度の分析に進むこともできます。
EDA　 EDA

時系列の分析

時系列の分析 は、大きく２つに分かれます。

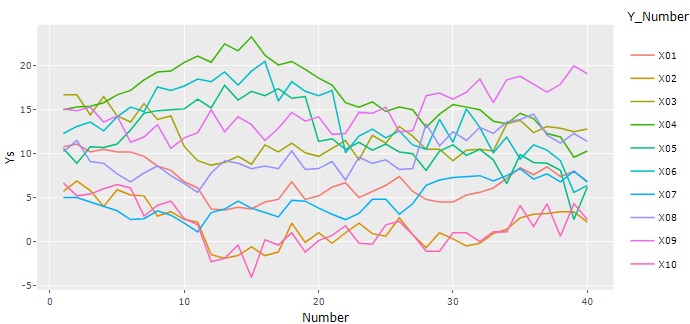
データの順番が時間の順になっていることが、よくありますが、１つ目は、この順番の特徴を見る分析です。 折れ線グラフ が基本ですが、データを加工すると、折れ線グラフで見えることが、いろいろと変わります。
EDA　 EDA

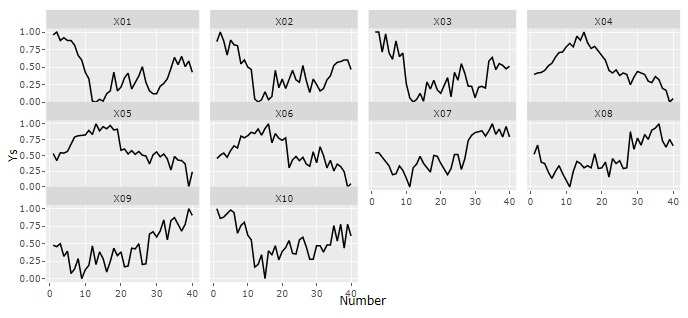
２つ目は、時刻を表すデータに基づいて、時間的な特徴を調べる方法です。 なお、こちらの分析は、その現象や時刻というデータの性質を見ますので、EDAよりも専門的な分析です。

ヒートマップ

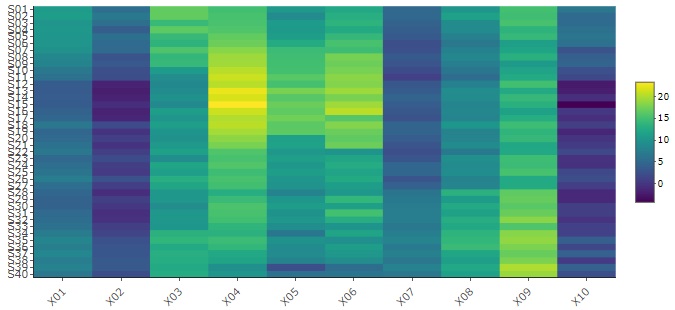
数値データだと使える技ですが、 ヒートマップ にして、データの表全体を可視化します。

データの並び方の特徴が見えることがあります。
EDA

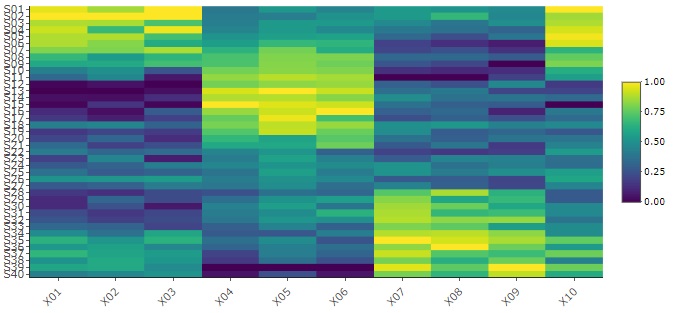
標準化 をしてからヒートマップを見ると、さらに理解が深まることもあります。
EDA

クラスター分析 で並び変える方法もあります。
EDA

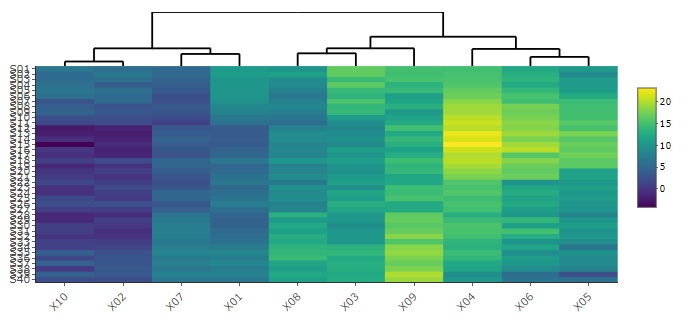
比較的規模の小さな表データでは、ヒートマップだけで、 変数の類似度の分析 、 サンプルの類似度の分析 、 多対多の分析 、 カテゴリの類似度の分析 、 時系列の分析 がいっぺんにできます。 これらの方法の補助的な方法としても使えます。

R-EDA1

R-EDA1は、筆者の実務で使って来たEDAを、誰でも手軽にできるようにしたフリーソフトです。 このページの例にした図は、このソフトで作っています。

Rをベースにしていますが、ノーコード（プログラミングなし）で使えます。 インストールや登録などの作業も不要です。

R-EDA1の起動

R-EDA1は https://ecodata222.shinyapps.io/R-EDA1/ にアクセスすると起動します。

R-EDA1の詳細

詳しい説明は、 ウェブアプリR-EDA1 のページにあります。

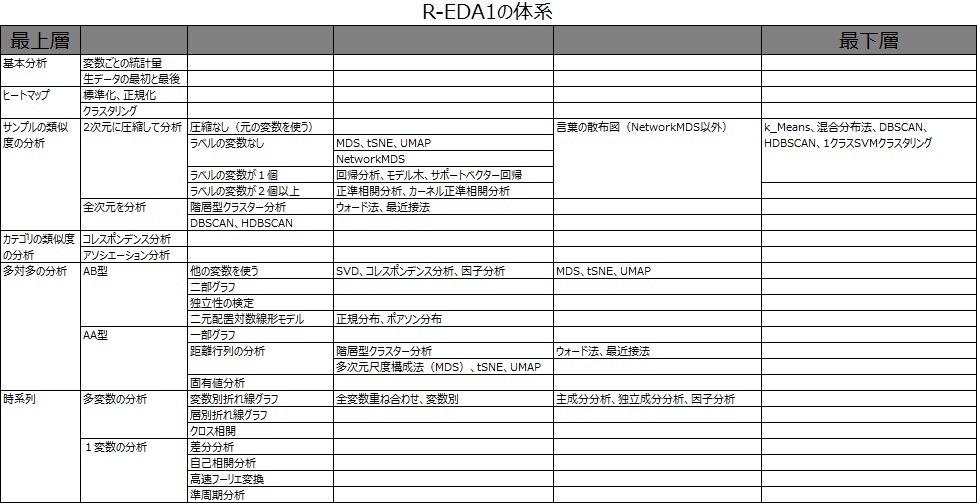
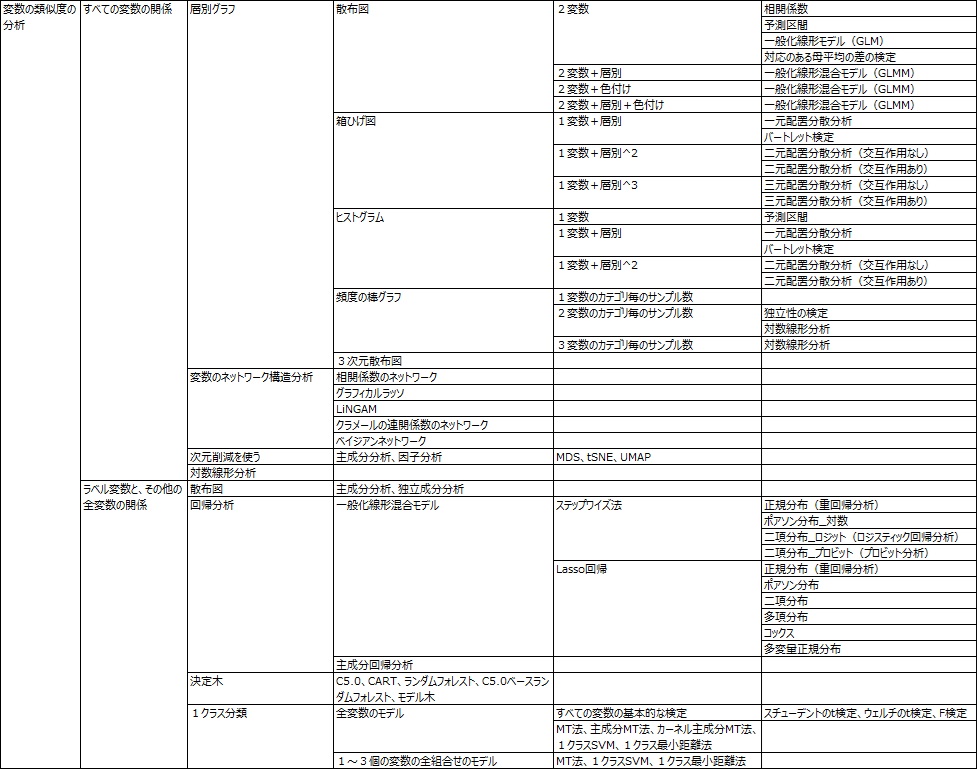
このページの上記の説明は、R-EDA1の最上層にある７本の柱の説明です。細かい体系は下図になっています。
ウェブアプリ　R-EDA1
ウェブアプリ　R-EDA1



参考文献

「データサイエンス講義」　Rachel Schutt・Cathy O'Neil　著　オライリー・ジャパン　2014
EDAは、すべての変数の分布をプロッし、時系列データをプロット、変数を変換、散布図行列を作成、全変数の要約統計量を計算するものして、 説明しています。




順路 次は 決定木

データサイエンス教室