 Rによるデータ分析
Rによるデータ分析
 Rによるデータ分析
Rによるデータ分析
カテゴリの分解分析 を、Rで進める時のレシピです。 Rによる分解分析 を質的変数用に改造しています。
主成分分析、 独立成分分析、 コレスポンデンス分析、 因子分析 をいっぺんにするコードです。
# データの読み込み
library(fastDummies)# ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- Data # 加工用のデータを作る
# 主成分分析
Data2 <- dummy_cols(Data1,remove_first_dummy = FALSE,remove_selected_columns = TRUE)# 因子分析ではエラーになる
pc <- prcomp(Data2, scale=TRUE,tol=0.01)# 主成分分析
Data3a<-pc$x# 要約変数(主成分)を抽出
Data4a<-cbind(Data2,Data3a)# 元データと合体
cor2all <- cor(Data4a)^2# 変数の組合せについて、寄与率(相関係数の2乗)を計算
ncol2 <- ncol(Data2)
ncol3 <- ncol(Data3a)
n3 <- ncol2 + 1
n4 <- ncol2 + ncol3
PCA <- round(cor2all[n3:n4,1:ncol2],4)
# 独立成分分析
Data2 <- dummy_cols(Data1,remove_first_dummy = FALSE,remove_selected_columns = TRUE)# 因子分析ではエラーになる
library(fastICA) # ライブラリを読み込み
ICA <- fastICA(Data2, ncol3)# 独立成分分析。抽出成分の数はncol3
Data3b <- ICA$S# 要約変数(独立成分)の抽出
Data4b<-cbind(Data2,Data3b)# 元データと合体
cor2all <- cor(Data4b)^2# 変数の組合せについて、寄与率(相関係数の2乗)を計算
ncol2 <- ncol(Data2)
ncol3 <- ncol(Data3b)
n3 <- ncol2 + 1
n4 <- ncol2 + ncol3
ICA <- round(cor2all[n3:n4,1:ncol2],4)
# コレスポンデンス分析
Data2 <- dummy_cols(Data1,remove_first_dummy = FALSE,remove_selected_columns = TRUE)# 因子分析ではエラーになる
library(MASS)
ca_result <- corresp(Data2,nf=ncol3)# コレスポンデンス分析。潜在変数の数をncol3と仮定
Data3c <- ca_result$rscore # ライブラリの読み込み
Data4c<-cbind(Data2,Data3c)# 要約変数の抽出
cor2all <- cor(Data4c)^2# 変数の組合せについて、寄与率(相関係数の2乗)を計算
ncol2 <- ncol(Data2)
ncol3 <- ncol(Data3c)
n3 <- ncol2 + 1
n4 <- ncol2 + ncol3
CA <- round(cor2all[n3:n4,1:ncol2],4)
# 因子分析
Data2 <- dummy_cols(Data1,remove_first_dummy = TRUE,remove_selected_columns = TRUE)# 質的変数があればダミー変換
ncol3c <- ncol3 # 下記でエラーが出たら、「ncol3-1」や、「ncol3-2」に書き換え
library(psych) # ライブラリの読み込み
fa_result <- fa(Data2, nfactors = ncol3c, fm = "ml", rotate = "varimax") # 因子分析。潜在変数の数をncol3cと仮定
Data3d <- fa_result$scores # ライブラリの読み込み
Data4d<-cbind(Data2,Data3d)# 要約変数の抽出
cor2all <- cor(Data4d)^2# 変数の組合せについて、寄与率(相関係数の2乗)を計算
ncol2 <- ncol(Data2)
ncol3 <- ncol(Data3d)
n3 <- ncol2 + 1
n4 <- ncol2 + ncol3
FA <- round(cor2all[n3:n4,1:ncol2],4)
PCA# 寄与率(相関係数の2乗)の表示
ICA# 寄与率(相関係数の2乗)の表示
CA# 寄与率(相関係数の2乗)の表示
FA# 寄与率(相関係数の2乗)の表示
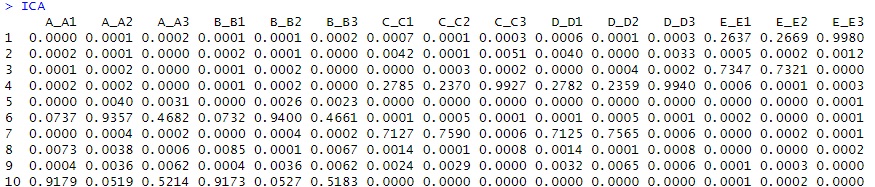
# 主成分分析
library(igraph)
pc4<-round(PCA,1) # 相関係数の2乗が0.1未満なら、0にする。
pc4<-pc4*5 # 相関係数の2乗は最大で1なので、最大の線の太さが10になるようにする
DM.g<-graph_from_incidence_matrix(pc4,weighted=T) # グラフ用のデータを作る
V(DM.g)$color <- c("steel blue", "orange")[V(DM.g)$type+1] # 色を変える
V(DM.g)$shape <- c("square", "circle")[V(DM.g)$type+1] # マークの形を変える
plot(DM.g, edge.width=E(DM.g)$weight) # グラフを作る
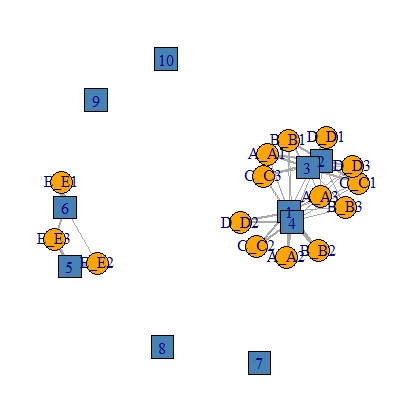
# 独立成分分析
library(igraph)
pc4<-round(ICA,1) # 相関係数の2乗が0.1未満なら、0にする。
pc4<-pc4*5 # 相関係数の2乗は最大で1なので、最大の線の太さが10になるようにする
DM.g<-graph_from_incidence_matrix(pc4,weighted=T) # グラフ用のデータを作る
V(DM.g)$color <- c("steel blue", "orange")[V(DM.g)$type+1] # 色を変える
V(DM.g)$shape <- c("square", "circle")[V(DM.g)$type+1] # マークの形を変える
plot(DM.g, edge.width=E(DM.g)$weight) # グラフを作る
# コレスポンデンス分析
library(igraph)
pc4<-round(CA,1) # 相関係数の2乗が0.1未満なら、0にする。
pc4<-pc4*5 # 相関係数の2乗は最大で1なので、最大の線の太さが10になるようにする
DM.g<-graph_from_incidence_matrix(pc4,weighted=T) # グラフ用のデータを作る
V(DM.g)$color <- c("steel blue", "orange")[V(DM.g)$type+1] # 色を変える
V(DM.g)$shape <- c("square", "circle")[V(DM.g)$type+1] # マークの形を変える
plot(DM.g, edge.width=E(DM.g)$weight) # グラフを作る
# 因子分析
library(igraph)
pc4<-round(FA,1) # 相関係数の2乗が0.1未満なら、0にする。
pc4<-pc4*5 # 相関係数の2乗は最大で1なので、最大の線の太さが10になるようにする
DM.g<-graph_from_incidence_matrix(pc4,weighted=T) # グラフ用のデータを作る
V(DM.g)$color <- c("steel blue", "orange")[V(DM.g)$type+1] # 色を変える
V(DM.g)$shape <- c("square", "circle")[V(DM.g)$type+1] # マークの形を変える
plot(DM.g, edge.width=E(DM.g)$weight) # グラフを作る

