二値データの寄与率

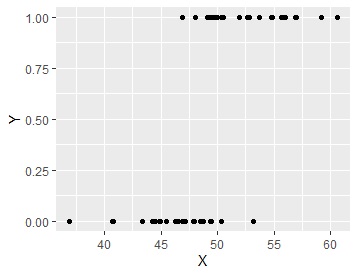
logistic
ロジスティック回帰分析が扱うのは、説明変数Xが連続変数、目的変数Yが0と1だけの二値データです。

普通の回帰分析では、良くない時

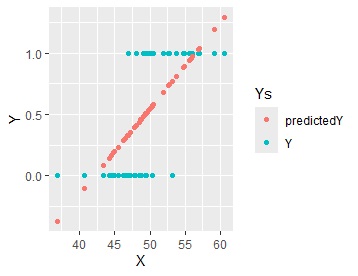
上のようなデータに対して、普通の回帰分析をすると、下の左図になります。目的変数Yは、0と1しかないのに、0から1の範囲よりも外の値が予測値になるので、変なモデルです。

ロジスティック回帰分析では、「だから、ロジスティック回帰分析のモデルを使いましょう」となります。ロジスティック回帰分析のモデルなら、右図のように、0から1の範囲に入るモデルになります。
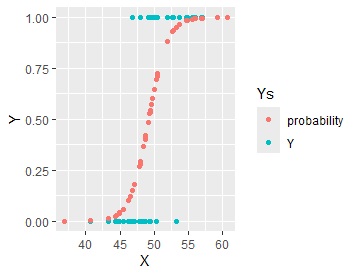
logistic

ところで、普通の回帰分析が良くないから、相関係数の計算も良くないのかというとそうでもないです。相関係数の2乗には、寄与率としての使い道がありますが、この値は、意味のある値です。

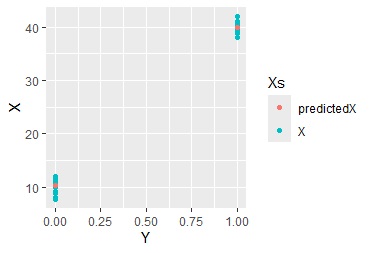
上のグラフで、XとYを入れ替えて、Xを目的変数、Yを説明変数として普通の回帰分析をすると、予測値は、Yが0と1の時の、それぞれの平均値になります。つまり、平均値を中心として、上下にばらついているモデルとして求まります。

このモデルで、Xのばらつきをどれだけ説明できているのかということが、寄与率の意味になっています。
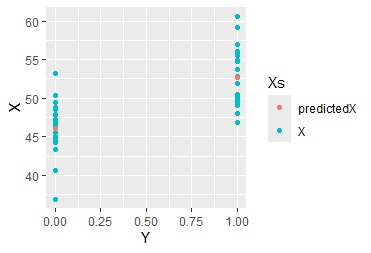
logistic

「２つの変数間に関係があるか？」ということを調べたい時は、回帰分析でどちらを目的変数にするのかということは、どちらでも良いです。そのため、「２つの変数間に関係があるか？」を調べる目的なら、二値データの時の寄与率は、意味のあるものとして活用できます。

例えば、上の例では、寄与率は、0.46です。下の例では、0.95です。下の例では、YとXに強い関係があることが、寄与率からわかります。
logistic