 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
自己組織化マップ(SOM : Self Organizing Map)は、 高次元を2次元に圧縮して可視化 の一種です。 サンプルの類似度の分析 に使います。
自己組織化マップでは、2次元への圧縮に、
ニューラルネットワーク
を使っています。
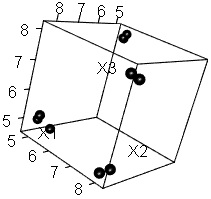
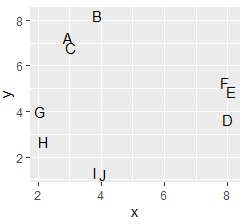
例えば、 主成分分析 では、データを変換する式を作って、変換します。 その結果、高次元の特徴が低次元で見えるようにしていきます。
自己組織化マップでは、例えば、「10×10」というように格子の数を決めて、 その格子の中に、それぞれのサンプルを割り振ります。
自己組織化マップでは、同じ格子に割り振られたサンプルは同じものとみなされます。 そのため、自己組織化マップは、 クラスター分析 としての一面も持っています。
ただ、一般的な クラスター分析 と違って、自己組織化マップでは、クラスターの近さが2次元マップでわかるようになっています。 このため、自己組織化マップは、 高次元を2次元に圧縮して可視化 と クラスター分析 の両方の特徴を併せ持った方法になっています。
上のRの例では、縦横が10ずつで、10×10の格子になっています。 この例のサンプル数と、サンプルの散らばり方だと、うまく結果が出ています。
まず、極端に少ない例として、元のデータが4つのグループに分かれているからということで、2×2や、4×1でもできそうな気もしますが、 間違った分類が起きます。
逆に、100×100にしたりすると、乱数を使わなくても、サンプルが適度に散らばるのですが、計算時間がとてもかかります。 格子の数を多くすると、 クラスター分析 としての特徴がなくなるのですが、そういう使い方はほぼ不可能です。
Rによる実施例は、 Rによる高次元を2次元に圧縮して可視化 のページにあります。
「自己組織化マップ 理論・設計・応用」 マーク・M.ヴァン・フッレ 著 海文堂 2001
生物の神経モデルとして自己組織化マップが考えられて来た話が、ずいぶんあります。
「自己組織化マップ」 T.コホネン 著 シュプリンガー・フェアラーク東京 2005
数学の基礎的なところから、事例まで、事典のように広くまとめられています。
「医療・医学・薬学におけるSOMの応用」 徳高平蔵・大北正昭・大藪又茂 監修 海文堂 2015
特定の分野でのSOMの事例をまとめています。
アンケートの解析や、脈波の解析もあります。
ちなみに、脈波は、データとしては「準周期的な時系列データ」になります。
東洋医学
や
複雑系
でも文献を見たことがあります。
18章が「固形製剤の開発」となっていて、
品質学
の分野の話でした。
既知の処方で実験データを取る → 応答曲面法
で、設計変数と製剤の特性の関係をモデル化 → 未知の処方の時の特性を予測 → 未知の処方の時の設計変数と特性の関係をSOMで解析、
という手順でした。
「自己組織化マップとその応用」 徳高平蔵・大北正昭・藤村喜久郎 編 シュプリンガー・ジャパン 2007
CD-ROMが付いています。
球面SOMを中心にした内容です。
「SOM」と言えば、2次元の平面のマップが一般的ですが、これだとマップに端がある事が、現実の問題と合わない事があるそうです。
そこで考え出されたのが、球面のマップになります。
筆者が興味を持ったのは、12、13章の脈波の解析、16章の変圧器の異常診断、17章のダムの土砂生産量、19章のマンガ家の解析です。
19章の解析は、まず、
多次元尺度構成法
では、好きか嫌いかを尋ねた回答のデータには良いけれども、「知らない」が大半を占めるデータを使って、
ニッチな事を調べる解析には、向かなかったそうです。
また、
相関ルール(アソシエーション分析)
では、大量のルールがわかったものの、全体像がわからなかったそうです。
449人のマンガ家を2次元マップにしてみるだけでも、驚きの結果だったそうですが、さらに球面SOMもしています。
「弱い紐帯」というものが、ネットワーク分析の理論の中にあるそうです。
これは、クラスター間のショートカットを指していて、伝達コストを大幅に下げる効果があるそうです。
球面SOMは、マクロな距離関係を計算する方法と考え、
相関ルールは、ミクロな共起関係を計算する方法と考えると、
距離が遠くて、共起が強いものは、「弱い紐帯」に相当すると考えます。
これは、「遠距離の仲良し」、「異ジャンルだが、支持者が共通」、「意外だが面白い」、と解釈します。
この研究では、ジャンルが異なるのに、共起が強いマンガ家の共通点として、同じ雑誌に連載されていた点に行き着いています。
「自己組織化マップとそのツール」 大北正昭・徳高平蔵・藤村喜久郎・権田英功 編 シュプリンガー・ジャパン 2008
編者が共通の上記の本とは異なり、ツールの解説が中心になっています。
ツールは、CD-ROMが付いています。
「データマイニング入門 :Rで学ぶ最新データ解析」 豊田秀樹 編著 東京図書 2008
自己組織化マップが、ひとつの章になっています。
サンプルコードや、サンプルデータもあり、Rを使って自分で試せるようにもなっています。
上記のRの実施例に、データを標準化する方法や、乱数を使ってずらす方法がありますが、この本を参考にさせていただきました。
このページでは、グラフのソフトの機能を使って、値の重なりをずらしていますが、
この本では、グラフに使うデータに乱数を足してばらつかせる方法を紹介しています。
「Rによるデータサイエンス」 金明哲 著 森北出版 2007
多変量解析
や
データマイニング
の様々な手法と、Rで実行する方法がコンパクトにまとまっています。
順路


 次は
近い・遠いだけに注目して2次元に圧縮する方法
次は
近い・遠いだけに注目して2次元に圧縮する方法

