上の式は ARIMAモデル の一種や変形と言えるような式です。 MAの部分がないです。 また、f()は、線形和以外の関数を想定しています。
原因と結果の関係として、「原因が先で、結果が後」という時間の観点は、常識的なものです。 統計的因果推論 では、式を作る時の メタ知識 として、その常識を使っています。 式の中に明示的に、その観点は入っていないです。
時系列解析 の 自己相関分析 では、時間的な観点を明示的に含んでいる理論ですが、「因果推論」の理論としては、あまり考えられていないです。
ARI因果効果モデルは、統計的因果推論にある 事実と反事実 や 因果効果 のアイディアを使いつつも、 自己相関分析 の式のアイディアを使っているものとして、筆者が考えてみたものです。
「ARI因果効果モデル」は、筆者の造語です。 名前もアイディアも、既に世の中にあれば、そちらに合わせますが、なさそうなので、この名前にしています。
上の式は
ARIMAモデル
の一種や変形と言えるような式です。
MAの部分がないです。
また、f()は、線形和以外の関数を想定しています。
ARI因果効果モデルの「ARI」は、ARIMAモデルの「ARI」から来ています。
下の式が、ARI因果効果モデルです。
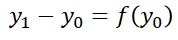
ARI因果効果モデルでは、
因果効果
は、Y1とY0の差分と考えます。
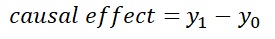
因果効果が一定なのを想定するのが、
因果効果の分析の例になります。
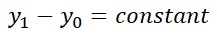
下の例の場合は、一定を想定しているけれども、一定値からのばらつきが、Y0とY1の両方であります。
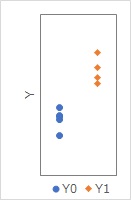
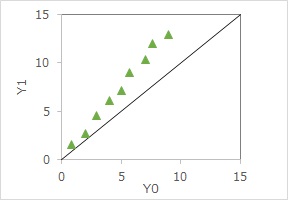
上のようなデータがあったとします。
Y0が処置無し、Y1が処置ありです。
Y0とY1の値が同じだと、斜め45度の線に乗るのですが、どの点も、その線の上なので、Y0よりもY1の方が必ず大きいことがわかります。
また、Y0が大きいほど、Y1は、その線よりも離れていることもわかります。
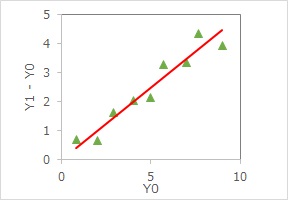
因果効果として「Y1-Y0」を計算してグラフにすると、下になります。
Y0が大きいほど、Y1とY0の差が大きいことを表しているグラフになっています。
ARI因果効果モデルの式として、下を想定します。
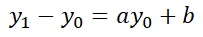
Y0の状態が今までの通常状態で、Y1はY0に対して何かの処置をした場合、モデルとしては、Y0とY0に何かをしたものが、Y1になっていると考えた方が良いです。 ARI因果効果モデルは、そのようなモデルとして作られています。
S-lernerでは、右辺に、Z=1の時の式が入りますが、ARI因果効果モデルでは入りません。T-lernerでも同様です。
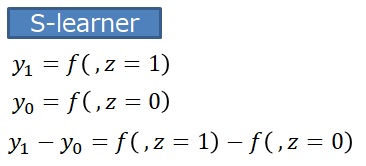
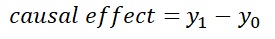
S-lernerは、Z=1と0の時の２通りが元々あって、因果効果はその差になっている時のモデルになっているので、 「Y0に何かをしたものが、Y1になっている」という考え方にはなっていません。
順路
次は
一般化因果効果モデル
