一般化因果効果モデル

ARI因果効果モデルは、時系列解析の ARIMAモデルを転用して、因果効果を扱えるようにしたモデルです。

このページは、このアイディアをさらに進めてみたものです。

下の式が、一般化因果効果モデルです。
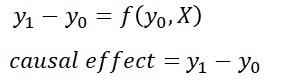
causal_effect
Y1とY0の差分が因果効果です。

目的変数が、因果効果になっているところは、 ARI因果効果モデルと同じです。因果の有無を、因果効果という量で評価します。

また、 ARI因果効果モデルと同じく、右辺のf()の中に、Y0が含んでいます。 Y1とY0が、右と左のように同等のものなら、不要かもしれませんが、Y0が「基準」や「現状」と言えるようなもの場合、入れて置いた方が良い変数になります。

ARI因果効果モデルと違うのは、f()の中にXが入っている点です。 Xは、原因系と考えている変数で、１個とは限らないです。

機械学習の一般的なモデルは、Y1やY0の片方を目的変数としてモデルを作るので、 Y1-Y0を目的変数とする発想はしていません。

一般化因果効果モデルは、Y1-Y0には、「因果効果」という意味があるものとして、モデルを作っています。

また、式の右辺と左辺の両方にY0が入るようなモデルの作り方は、普通はしないです。

反事実のデータが仮想的な場合

仮想的な反事実の分析のように事実と反事実の分析では、反事実のデータはない場合があります。

上記の一般化因果効果モデルは、事実と反事実の両方のデータがそろっていることを前提としているので、反事実のデータがなければ使えません。

そのような場合、 T-lerner で、反事実のデータを推定するという作業を前処理として行う方法が考えられます。

T-lernerやS-lerner は、Y1やY0についての式が求まります。そのため、反事実のデータ（Y1とY0のいずれか）がないサンプルについて、因果効果の値（Y1-Y0）を計算できるようになります。

しかし、因果効果のY1-Y0の式が求まる訳ではないので、「結局のところ因果効果はどのようなモデルで考えれば良いのか？」という疑問には答えられないです。

一般化因果効果モデルは、この疑問に答えるモデルになります。

T-lernerとうまく組み合わせると、反事実のデータが存在しないケースでも、一般化因果効果モデルは作れます。