Xという変数は、Yの原因ではないけれども、Yとの相関が高く、
疑似相関
の関係がある時に使える方法です。
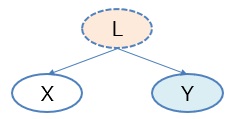
上図のような時は、 因子分析 をすると、Lをあぶり出すことができることがあります。
主成分分析 や 独立成分分析 も同じ目的で使えることがあります。
方法の違いは、 分解分析の違いのページにあります。
疑似相関からの因果推論のポイントは、YとXを区別せずに、因子分析をするところです。
ところで、Y、X1、X2という変数があると、
Yを目的変数、X1、X2を説明変数として、モデルを作りたくなります。
例えば、下のようなモデルです。
Y = A1 * X1 + A2 * X2 + B
実際、下のようなデータの構造の時は、このモデルが精度の高いモデルになることもあります。
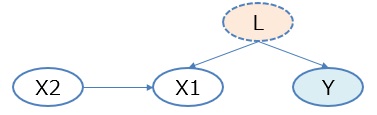
この場合は、X1の中に入っているX2の要素を引き抜いて、Lを見えないところであぶり出しているので、精度の高いモデルになるのですが、 それは注意深く係数を見たりしないと、気付けないので注意が必要です。
精度の高いモデルにはなりますが、実際の現象の中ではYとは関係のないX2が、Yに影響しているモデルになるため、結果の考察で困ることになります。
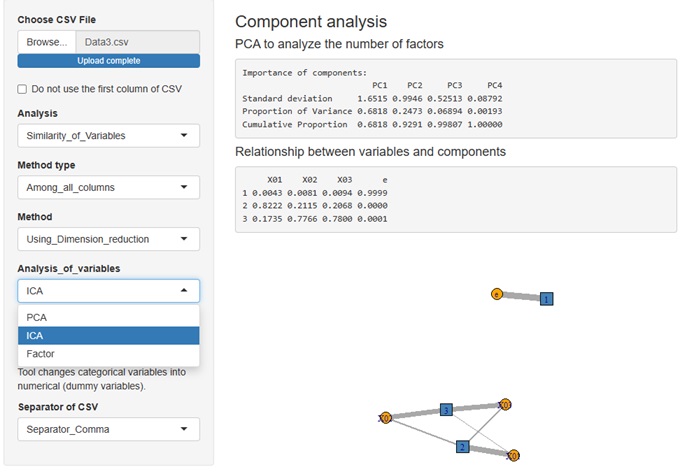
Rによる分解分析 では、主成分分析、独立成分分析、因子分析で求める各要約変数の寄与率だけを比較する分析の実施例があります。
R-EDA1
では、３つの手法を選べます。
順路
次は
隠れ変数の探索
