潜在変数の因果推論 をするにあたって、モデルは大きく２つに分かれます。
いずれも、目的変数と説明変数に共通の潜在変数があるとするモデルなのは一緒なのですが、 潜在変数の求め方が違います。
共通して言えるのは、潜在変数を想定しない普通の重回帰分析のモデルで、結果の考察が難しい時に役に立つことです。 疑似相関からの因果推論 にもありますが、 「単純に重回帰分析をした時に、精度の高いモデルにはなった。しかし、実際の現象の中ではYとは関係のないX2が、Yに影響しているモデルになるため、結果の考察ができない。」というケースで、役に立ります。
ひとつは、 疑似相関からの因果推論 にあるように、目的変数と説明変数を区別しないで扱うモデルです。
手順としては、目的変数と説明変数を一緒にして、 因子分析 や 独立成分分析 をして、潜在変数を求めます。
もうひとつは、 主成分回帰分析による因果推論 にあるように、目的変数と説明変数を区別して扱うモデルです。
手順としては、まず、説明変数だけで、 因子分析 や 独立成分分析 をして、潜在変数を求めます。
次に、潜在変数と目的変数の関係を調べます。
同じデータについて、２つのモデルで比べたのが、下の例になります。 上側が、目的変数と説明変数を区別して扱うモデル（因子回帰分析）です。 下側が、目的変数と説明変数を区別しないモデル（因子分析）です。
違いは、区別しないモデルの方は、Yに、成分がひとつ多く付いている点です。
Yだけにある誤差項の成分が大きいと、このような違いになります。
区別するモデルの方は、成分を説明変数として重回帰分析をした時に、成分では説明しきれない残差の大きさが、この誤差項ということになります。
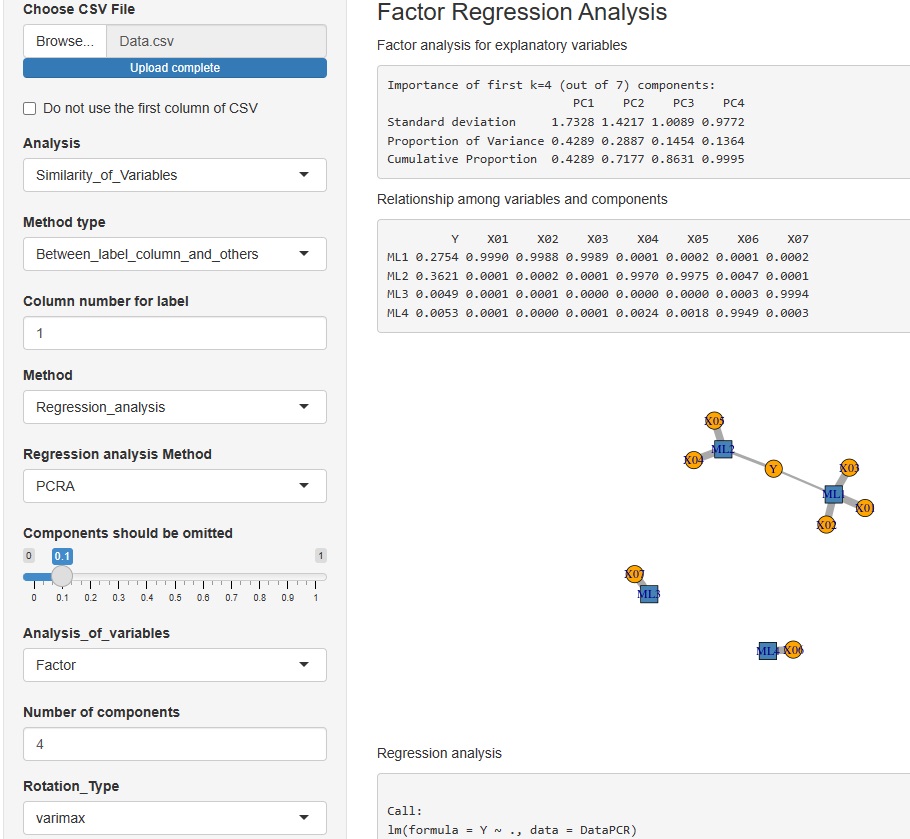
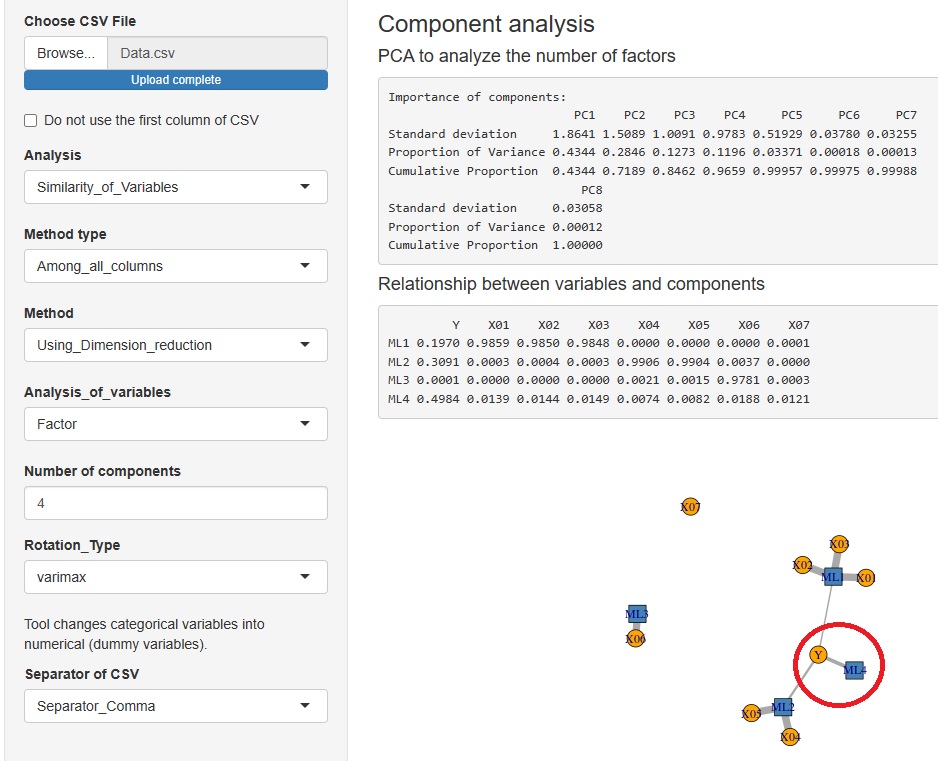
上の例だけだと、「区別しないモデルの方が便利」ということになります。 区別するモデルと、区別しないモデルの比較は、 独立成分分析のみによる独立成分回帰分析 のページにもありますが、「違いはない」と言える結果になっています。 主成分分析のみによる主成分回帰分析 のページだと違いが見られます。 主成分分析を使う場合は、区別した方が良いようです。
区別するモデルは、 Rによる主成分回帰分析 のページです。 区別しないモデルは、 Rによる分解分析 のページです。
上の例は、 R-EDA1 で実施しています。
順路
次は
量質混合の潜在変数モデル
