主成分分析のみによる主成分回帰分析（RAOPCA）

主成分回帰分析では、説明変数を主成分分析してから、その主成分を説明変数にして、重回帰分析をします。

予測モデルを作りたいのなら、この手順になるのですが、因果関係の分析で主成分回帰分析を使う時は、「主成分分析だけで主成分回帰分析」という方法が可能です。

「主成分分析のみによる主成分回帰分析」という名前は長いので、以下、RAOPCA（Regression Analysis Only Parctial Component Analysis）という名前にします。

ちなみに、主成分回帰分析の略称は、PCR（Parctial Component Regression Analysis）と呼ばれることが多いです。

RAOPCAの手順

目的変数と説明変数を一緒にして、主成分分析をします。

次に、それぞれの変数と、それぞれの主成分についての組合せについて、寄与率（相関係数の２乗）を計算します。分析するのは、この値になります。

主成分回帰分析では、目的変数とそれぞれの主成分について求めた相関係数の２乗は、それぞれの主成分の目的変数への寄与率としての意味を持っています。足し合わせると、１以下になります。

個別の因子の寄与率のページにもあるように、一般的な重回帰分析では、個々の説明変数と相関係数の２乗は、寄与率として使えません。足し合わせると１よりも大きくなることもあります。

しかし、主成分では、事情が違って来ます。 RAOPCAは、この性質を利用します。

RAOPCAで求める主成分は、求め方が違うので、主成分分析回帰分析とまったく同じにはならないのですが、目的変数とそれぞれの主成分について求めた相関係数の２乗の性質は、主成分回帰分析と同じです。ここで「同じ」となる点が、主成分分析のみで主成分回帰分析ができる理由になります。

RAOPCAは、古くて新しい方法です。

まず、主成分分析も、主成分回帰分析も、今は古典的な方法と言えるようなものです。この点が古いです。

元の変数と主成分の相関係数は、「因子負荷量」という名前で知られています。この相関係数を分析に使う点も古いです。

一方、「主成分分析で主成分回帰分析と同じ分析をする」という発想は、もしかしたら、既にどなたかが論文にしているかもしれませんが、筆者の知る限りでは、見たことがないです。少なくとも、ポピュラーな分析方法ではないです。この点が新しいです。

RAOPCAは、相関係数（因子負荷量）を２乗にしたものを分析します。２乗するだけなのですが、相関性と相関係数のページにもあるように、相関係数の２乗には、寄与率としての意味があります。 RAOPCAは、この特徴を利用します。これを分析の中心にする点も新しいです。

主成分回帰分析（PCR）、部分的最小二乗回帰分析（PLS）、 RAOPCAの比較です。結論から書くと、RAOPCAは、PCRと似る場合と、PLSと似る場合があります。どちらに似るのかは、データによるようです。

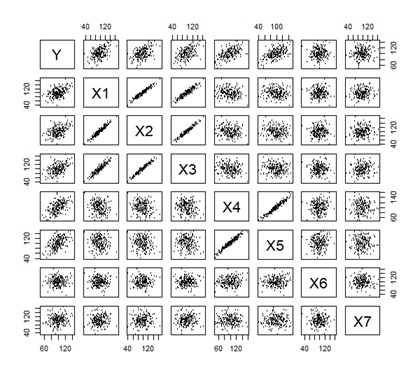
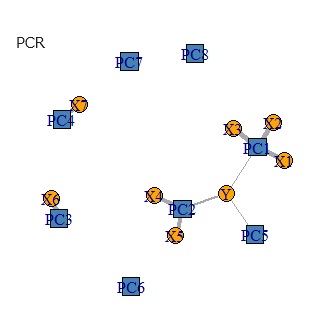
下の図は、左から順に、データ、PCR、PLS、RAOPCAです。
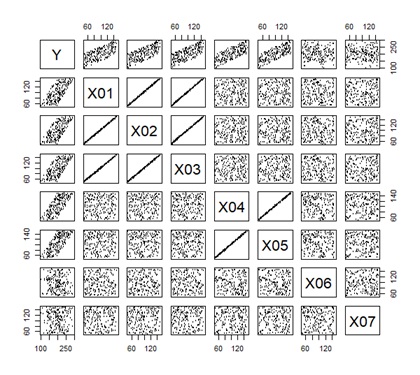
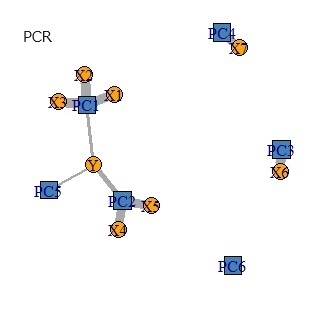
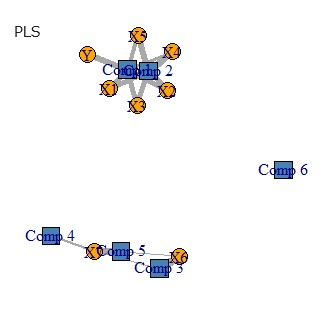
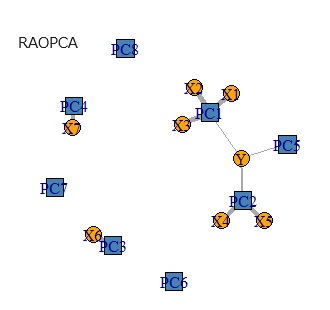
Data PCR PLS RAOPCA

Yからつながる主成分が、３つあるところは、PCRとRAOPCAで似ています。 PLAS場合は、１つだけです。

下の図は、左から順に、データ、PCR、PLS、RAOPCAです。
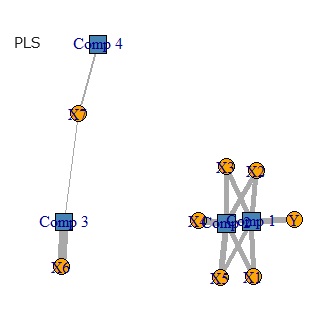
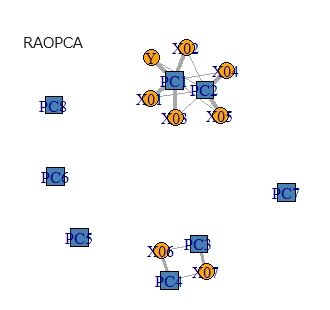
Data PCR PLS RAOPCA

Yからつながる主成分が、太い線で１つあるところが、RAOPCAとPLSで似ています。

部分的最小二乗回帰分析（PLS）のページで、「PLSよりもPCRの方が、因果関係の分析には使いやすい」という説明をしています。

この目的では、PCRではなく、PLSに似る場合のあるRAOPCAは、使いにくい方法です。

使い道があるとすれば、独立成分分析のみによる独立成分回帰分析（RAOICA）で計算がいまいちな時の、補助的手段かもしれません。