Rによるデータ分析
Rによるデータ分析
 Rによるデータ分析
Rによるデータ分析
近傍法 をベースにした異常の定量化です。
MT法と違って、特定の分布を仮定しないことが利点になります。 その代わり、単位空間のデータの個々の値に敏感に反応するので、 MT法をベースにした方法と比べると、単位空間のデータの内容のチェックがとても大事になります。
このページのコードは、入力データに「Y」という名前の変数が入っていることを想定しています。
「Y」の変数は、「0」と「1」の2つの数値が入っていることを想定しています。 「0」のサンプルは、単位空間であることを想定しています。 「0」のサンプルだけでモデルが作られます。
「1」のサンプルは信号空間です。 単位空間のデータに対して、異常なのかを見たいデータになります。
Y以外の変数は、名前に決まりはありません。
計算結果はグラフになるようにしましたが、定量的な結果として、誤判別になるサンプル数がわかるようにもしてみました。 最後に出てくる数値がそれです。
LOF を使う方法です。
下記のコードを使う場合、「Y = 1」のサンプルは1個が基本です。 2個以上でも計算はできますが、正常値から見たら「異常」でも、異常値同士が近いと「正常領域」と計算上は判定される可能性があります。
「Y = 1」が複数の時は、1個ずつLOFの計算を回す方法ができなくもないのですが、 ただでさえ計算時間が長いのに、それが「Y = 1」のサンプル数の分、倍増することになります。 そこまでする利点がないように思いましたので、 コード例を掲載するのはやめました。
library(Rlof)# ライブラリを読み込み
library(dummies) # ライブラリを読み込み
library(ggplot2) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- Data # 加工用のデータの作成
Y <- Data1$Y# Yのデータを別に作る
Data1 <- dummy.data.frame(Data)# 質的変数はダミー変換
Data1$Y <- NULL # Yの列を消す
Data2 <- subset(Data1, Data$Y == 0)# Yが0のサンプルのデータを別に作る
model <- prcomp(Data2, scale=TRUE, tol=0.01)# Yが0のサンプルのデータで主成分分析のモデルを作る。
Data3 <- predict(model, as.matrix(Data1))# 主成分得点を取る
std <- apply(model$x, 2, sd)# 列ごとに標準偏差を計算
Data4 <- Data3# 加工用のデータの作成
for (i in 1:ncol(Data3)) { # ループの始まり。データの列数を数えて同じ回数繰り返す
Data4[,i] <- Data3[,i]/std[i]# 標準化
} # ループの終わり
Data4 <- cbind(Data4 ,Y) # データを合体
LOF <- lof(Data4,5) # LOFを計算(5個の近傍点を使う)
Data8 <- as.data.frame(cbind(LOF ,Data))# データを合体
Data8$Y <- factor(Data8$Y)# Yの列を文字型にする
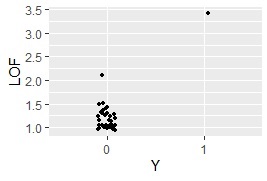
ggplot(Data8, aes(x=Y, y=LOF)) + geom_jitter(size=1, position=position_jitter(0.1))# 一次元ジター散布図を描く
1クラス最小距離法 を使う方法です。
library(dummies) # ライブラリを読み込み
library(ggplot2) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- Data # 加工用のデータの作成
Y <- Data1$Y# Yのデータを別に作る
Data1 <- dummy.data.frame(Data)# 質的変数はダミー変換
Data1$Y <- NULL # Yの列を消す
Data2 <- subset(Data1, Data$Y == 0)# Yが0のサンプルのデータを別に作る
model <- prcomp(Data2, scale=TRUE, tol=0.01)# Yが0のサンプルのデータで主成分分析のモデルを作る。
Data3 <- predict(model, as.matrix(Data1))# 主成分得点を取る
std <- apply(model$x, 2, sd)# 列ごとに標準偏差を計算
Data4 <- Data3# 加工用のデータの作成
for (i in 1:ncol(Data3)) { # ループの始まり。データの列数を数えて同じ回数繰り返す
Data4[,i] <- Data3[,i]/std[i]# 標準化
} # ループの終わり
Data5 <- dist(Data4, diag = TRUE, upper = TRUE)# サンプル間の距離を計算
Data5 <-as.matrix(Data5)# 行列形式に変換
diag(Data5) <- 1000 # 対角成分をとても大きな値にする
Data5 <-as.data.frame(Data5)# 形式を変換
Data5 <- cbind(Data5 ,Y) # データを合体
Data6 <- subset(Data5, Data5$Y == 0)# Y# Yが0のサンプルのデータを別に作る
Data6$Y <- NULL# データからYの列を消す
Data7 <- as.data.frame(t(Data6))# データを転置
min0 <- apply(Data7, 1,min)# 各行の最小値を計算
Data8 <- as.data.frame(cbind(min0 ,Y))# データを合体
Data8$Y <- factor(Data8$Y)# Yの列を文字型にする
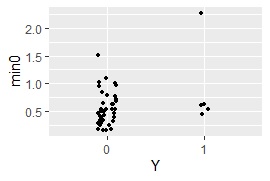
ggplot(Data8, aes(x=Y, y=min0)) + geom_jitter(size=1, position=position_jitter(0.1))# 一次元ジター散布図を描く
MaxMDinUnit <- max(subset(Data8, Data8$Y == 0)$min0)# Yが0のサンプルのmin0のMaxを求める
Data9 <- subset(Data8, Data8$Y == 1)# Yが1のサンプルを抜き出す
nrow(subset(Data9, Data9$min0 < MaxMDinUnit))# Yが1で、Yが0のサンプルのmin0のMaxよりも小さなサンプル数を求める