データは、上のようなものです。 サンプル数は、約1000あります。 A、B、C、Dは、３水準系の直交表です。 独立しています。
連関係数を使った主成分分析 のRによる実施例です。 Rによる連関係数分析 と前半部分は同じです。
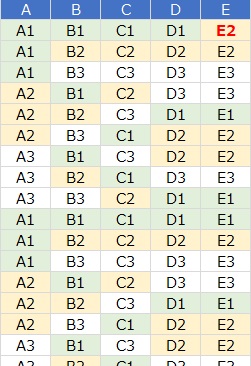
データは、上のようなものです。
サンプル数は、約1000あります。
A、B、C、Dは、３水準系の直交表です。
独立しています。
Eは、１行目が「E2」となっている以外は、並び方が、Dと、まったく同じになっています。
基本的に質的変数を扱う方法ですが、量的変数は １次元クラスタリング の方法で、質的変数に変換するコードが入っているので、 質的・量的が混合していたり、量的変数だけでも使えるようにしてあります。
library(vcd) #ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- Data # １次元クラスタリングの出力先を作る
n <- ncol(Data1) # データの列数を数える
for (i in 1:n) { # ループの始まり。データの列数を数えて同じ回数繰り返す
if (class(Data1[,i]) == "numeric") { # 条件分岐の始まり
Data1[,i] <- droplevels(cut(Data1[,i], breaks = 5,include.lowest = TRUE))# ５分割する場合。量的データは、質的データに変換する。
} # if文の処理の終わり
} # ループの終わり
GM2 <- matrix(0,nrow=n,ncol=n) # 出力先を作る
for (i in 1:(n-1)) { # ループの始まり
for (j in (i+1):n) { # ループの始まり
cross<-xtabs(~Data1[,i]+Data1[,j],data=Data1)# 分割表の作成
res<-assocstats(cross)# 連関分析
cramer_v<-res$cramer# クラメールの連関係数の抽出
GM2[i,j] <- cramer_v# クラメールの連関係数の書き込み
GM2[j,i] <- cramer_v# クラメールの連関係数の書き込み
} # ループの終わり
} # ループの終わり
rownames(GM2)<-colnames(Data1) # 行名をつける
colnames(GM2)<-colnames(Data1) # 列名をつける
diag(GM2) <- 1 # 対角成分を１にする
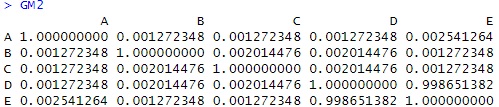
GM3 <- GM2
GM3[GM3 < 0.01] <- 0 # 連関係数の小さいものは0にする。
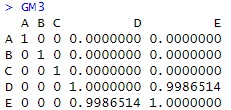
Eigen_analysis <- eigen(GM3) # 固有値分析
EA1 <- Eigen_analysis$values/sum(Eigen_analysis$values) # 全体への、各主成分の寄与率？
EA1
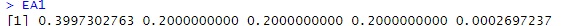
EA2 <- round(((sweep(Eigen_analysis$vectors, MARGIN=2, sqrt(Eigen_analysis$values), FUN="*")))^2,4) # 各変数への、各主成分の寄与率
rownames(EA2)<-colnames(Data1) # 列名をつける
EA2
# A、B、Cには、ひとつの主成分だけが対応しています。
D、Rは、２つの主成分が寄与率0.5ずつで対応しています。
library(igraph)
pc4<-round(EA2,1)
colnames(pc4)<- colnames(as.data.frame(pc4))
pc4<-pc4*10
DM.g<-graph_from_incidence_matrix(pc4,weighted=T)
V(DM.g)$color <- c("steel blue", "orange")[V(DM.g)$type+1]
V(DM.g)$shape <- c("square", "circle")[V(DM.g)$type+1]
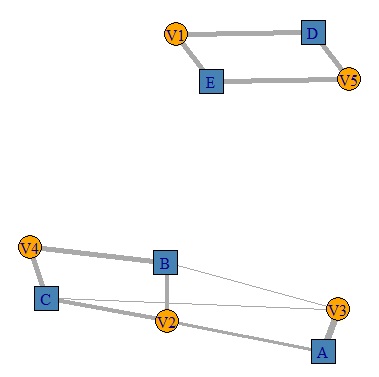
plot(DM.g, edge.width=E(DM.g)$weight)
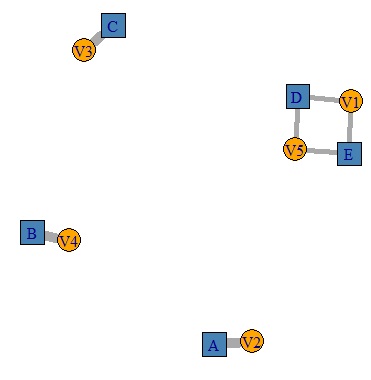
GM2からGM3を作るところがノウハウになっています。
GM2で、値の小さな連関係数を０にしておかないと、けっこう効いてしまい、本当は、ないところに関係があるような結果になってしまいます。
