Rによる主成分分析の基本 にあるA-B型の分析の続きです。
Rによる主成分分析の基本 のコードと、以下は同じです。
setwd("C:/Rtest")
Data <- read.csv("Data.csv", header=T)
DataName <- Data$Name # Nameの列を別名で保管する
Data$Name <- NULL # データからNameの列を消して、Xの列だけにする
pca_model <- prcomp(Data, scale=TRUE) # 主成分分析
summary(pca_model) # 「Cumulative Proportion」が累積寄与率。
pca_data1 <- as.data.frame(pca_model$x) # 主成分得点を得る
pca_dataA <- transform(pca_data1 ,name1 = DataName,Group = "A")# サンプル名を追加
pca_data2 <- sweep(pca_model$rotation, MARGIN=2, pca_model$sdev, FUN="*") # 因子負荷量を計算
pca_dataB <- transform(pca_data2 ,name1=rownames(pca_data2),Group="B")# 言葉の散布図
biplot(pca_model) # グラフを作る
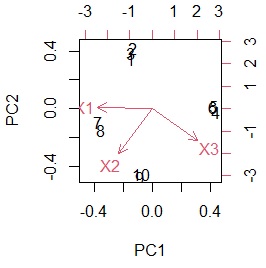
主成分との関係の情報は不要で、類似度だけを詳しく調べたい場合は、 多次元尺度構成法 を使って、 多数の主成分を２つに凝縮すると良いです。
なお、主成分の値ですが、変数については、-1から1までの値になります。 サンプルについては、0が中心ですが、-1から1までの範囲よりも広くなります。
上のグラフのように、２つの主成分を軸にして同時付置図を作った場合は、座標に意味があります。 特に主成分の場合は、0を中心とした見方ができます。
高次元を２次元に圧縮する方法を使った場合、この見方ができなくなります。 そのため、下記の手順で、すべての主成分の情報を持った多次元同時付置図を作ることはできますが、 この図からは、何も情報が得られないような気がしています。
library(MASS)# ライブラリを読み込み
Data1 <- rbind(pca_dataA,pca_dataB)# データを結合
pca_data11 <- Data1[,1:ncol(pca_data1)]
row.names(pca_data11) <- Data1$name1
Data11_dist <- dist(pca_data11)# サンプル間の距離を計算
sn <- sammon(Data11_dist) # 多次元尺度構成法
output <- sn$points# 得られた2次元データの抽出
Data2 <- cbind(output, Data1) # 元データと多次元尺度構成法の結果を合わせる。
ggplotly(ggplot(Data2, aes(x=Data2[,1], y=Data2[,2],colour=Group, label=row.names(pca_data11))) + geom_text()) # 言葉の散布図
