MT法の手順 のページでは、 単位空間 と信号空間のそれぞれについて、 マハラノビスの距離 （MD）を求めています。
異常状態の判定に MT法 を使うためには、もう一段階、やる事があります。
サンプルファイル には、３つの方法による判定の機能も付けました。
MT法 では、 単位空間 は、「正常のデータ」と考えますので、素直に 「単位空間のMDの最大値よりも大きければ異常」と考えるアプローチです。
実際のデータは、きれいな分布をしない事が多いので、筆者自身としては、この方法が良い事が多いです。
単位空間のMDの最大値よりも大きければ、「C」と判定する事にします。 当然の事ながら、単位空間（学習データ）のMDが「C」と判定される事はありません。 「C」に判定される可能性があるのは、テストデータだけです。
参考までに、「A」と「B」の判定も考案しました。 両方とも、単位空間の範囲には入りますので、「正常」の判定です。 単位空間のMDの平均値は、「1」になりますので、1よりも大きいかどうかが「A」と「B」 の違いになります。 単位空間のMDが「A」ばかりの場合、「B」と判定されたデータは、 異常に外れているデータの可能性があります。
下の図は、この方法のイメージです。
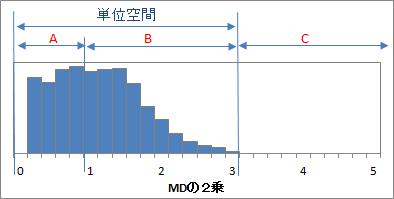
見た目でもわかりますが、 マハラノビスの距離 の分布は、 正規分布から作られるけど、正規分布ではない分布 の一種になります。
この分布は、カイ二乗分布で近似して、異常値の判定ができます。
MT法で使うMDは マハラノビスの距離 のページの定義２なので、カイ二乗分布そのままではなく、カイ二乗分布を変数の数で割った値の分布と考えます。
このMDの右側の累積確率は、Excelでは、
=CHIDIST(MD*変数の数,変数の数)
で計算する事ができます。
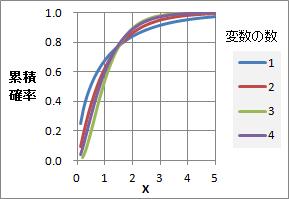
変数の数によって、分布の形が多少異なるものの、「MDが１くらいだとよくあることで、MDが４より大きい領域は、確率がとても低い」という程度は、 変数の数に関わらず、共通しています。
文献がわからないのですが、ネットで見かけた情報では、
品質工学
の中では、
MD > 4
が、異常かどうかの判定基準になっているようです。
カイ二乗法の図で、X=4の位置の累積確率は、変数が多いほど、限りなく1に近付いている事がわかります。
MT法では、変数の数で割った値をMDとして使うので、変数の数が変わっても、ひとつの値で判定する事が可能になっているようです。
順路
次は
MT法による異常の原因分析
