コレスポンデンス分析 は、一部の分野では有名ですが、 多変量解析 や 機械学習 の手法として紹介されることは、一般的ではないです。 一方、 主成分分析 は、 多変量解析 や 機械学習 の手法として紹介されることが一般的です。
ところが、これらの両者は、とても似ています。
コレスポンデンス分析と主成分分析は、手間はほとんど同じです。 結果も、とても似ています。
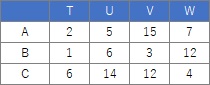
まず、
分割表
をデータのスタートにした場合の結果です。
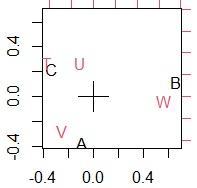
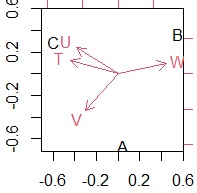
左がコレスポンデンス分析で、右が主成分分析です。
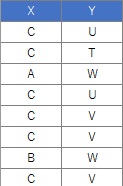
次に、上の分割表の元データをスタートにした場合の結果です。 コレスポンデンス分析は、分割表の分析法として知られていますが、分割表の元データを ダミー変換 したデータを入力データにしても、ほぼ同じ結果になります。
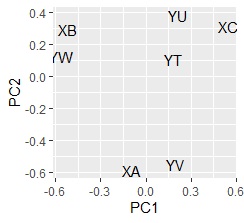
左がコレスポンデンス分析で、右が主成分分析です。
分割表を入力データにした時と、X軸の向き反対になる点も、２つの手法で同じです。
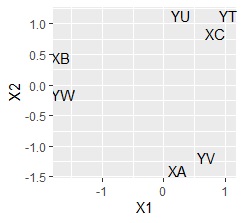
コレスポンデンス分析と主成分分析は、似たような結果が出るので同じように使っても問題のない時もありますが、 問題がある時もあります。
主成分分析の代わりにコレスポンデンス分析を使う場合ですが、 コレスポンデンス分析は、質的データを頻度データとして扱う理論で作られているので、量的データを扱う時に問題が起きます。 主成分分析では、温度と圧力など、単位のまったく異なる変数を一緒にしていても問題なく分析できますが、 これをコレスポンデンス分析で扱おうとすると、単位の異なる値を直接足し合わせる処理が入るため、想定外の使い方になります。
コレスポンデンス分析の代わりに主成分分析を使う場合については、「これは絶対にダメ」というのは、今のところ、筆者にはわかりません。 ただ、計数データに多次元正規分布を仮定するのは、どうかと思いますので、その点が大きく影響する場合は、問題が起きるかもしれません。 質的変数のグループを、１つの連続変数に変換 の方法として使う時は、コレスポンデンス分析の方が良いようです。
コレスポンデンス分析では、ひとつの変数群が ダミー変換 で複数の変数に分かれても、 グループが３つ以上の 正準相関分析 と似たアプローチになっているので、元の変数ごとのグループとして扱われます。
主成分分析の場合は、ひとつの変数がダミー変換されて複数の変数に分かれると、元の変数が何であったのかは関係なく、 変換後の変数は同じように処理されます。
コレスポンデンス分析の結果の分析方法として、散布図を使うのが一般的ですが、第１、第２の成分しか見ないことが多いようです。 実際問題として、第３以上の成分も分析しようとすると、グラフが２枚以上になってしまい、意思決定に使いにくい分析になってしまう問題もあります。
ちなみに、この問題は 主成分分析 と同じです。
順路
次は
質的変数のコレスポンデンス分析
