上のような質的変数のデータがあったとします。
このページは 尺度構成法 の一種です。 ２値変数のグループを、１つの連続変数に変換 と似ています。
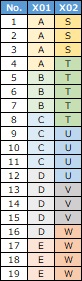
上のような質的変数のデータがあったとします。
質的データの相関性 の見方をすると、「X01とX02は相関が高い」というデータになっています。
A、B、C、D、EとS、T、U、V、Wというカテゴリがあり、「AとSは一緒になることが多い」、「BとTは一緒になることが多い」といったことはわかりますが、 それ以上はわかりません。
唐突ですが、このデータに コレスポンデンス分析 をすると、以下の２つのこともわかります。
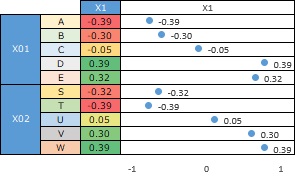
ひとつ目は、各サンプルの数値データです。
ダミー変換
のような1-0の離散値ではなく、小数点以下も細かくある数値になっています。
このページでは、このような数値の変数を「連続変数」と呼んでいます。
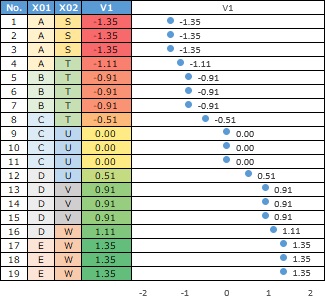
ふたつ目は、各カテゴリの数値です。
この例では、アルファベット順と、数値の順番が同じになっていますが、それはたまたまです。
例えば、上のデータでSとTが入れ替わっていると、一番小さな数値はTになります。
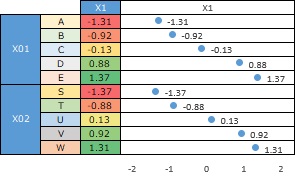
このようにして質的変数は、量的変数として扱えるようになります。
コレスポンデンス分析 の一般的な使い方では、「AとSだけが一緒になることが多い」というようなデータでも良いのですが、 このページの方法を使うには、他のカテゴリでも似た状態になっていて、質的変数同士の相関が高くなっている必要があります。
また、相関が高いといっても、下のデータのように、２つの変数のカテゴリ同士が完全に一致している場合は使えません。
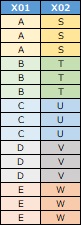
また、カテゴリには順序がある必要があります。 このようなデータは、潜在変数のようなものがあって、２つの質的変数が同じ潜在変数を背後に持っているような場合が考えられます。
コレスポンデンス分析 をすると、上記のV1のような変数だけでなく、V2やV3といった変数も出力されます。
一般的には、例えば、V1とV2の２次元の散布図を作って、各サンプルの類似性などを分析します。
ところが、このページの方法は、V1だけを拾います。 これを定量的な尺度として利用していくための、 特徴量エンジニアリング の一種になっています。
２値変数のグループを、１つの連続変数に変換 の方法と似ていて、１通り（１変数）の評価だけだと、大雑把な評価しかできないような場合に、 複数の変数を用意して、精度の高い数値データを得て行く方法になっています。
なお、上記では２変数ですが、３変数以上でもできます。
項目反応理論 には、質的変数が３値以上の方法として、順序がある場合の段階反応モデルはあります。 このページの方法は、それと似たアウトプットが得られる方法になっています。
段階反応モデルのソフトウェアは、カテゴリの辞書的な順番になっている順序尺度のデータとして処理するのですが、 このページの方法だと、カテゴリの辞書的な順番の情報は使いません。 順序の情報は、データから読み取るようになっています。
ファジィ理論 だと、カテゴリと数値の関係は、人が決める必要がありますが、 このページの方法だと、データから計算で数値が求まります。
このページでは、コレスポンデンス分析をした時に作られる第１の変数が、質的変数の背後にある潜在変数と解釈して利用します。 順序尺度の情報をデータから読み取ります。
「なぜ、こんなことができるのか？」というのは、筆者はわかっていません。 ただ、いろいろ試しても、必ずそうなったことと、 数量化Ⅲ類 は、もともとデータのそういう性質を定量化する方法として開発されたものなので、間違ったことはしていないようです。
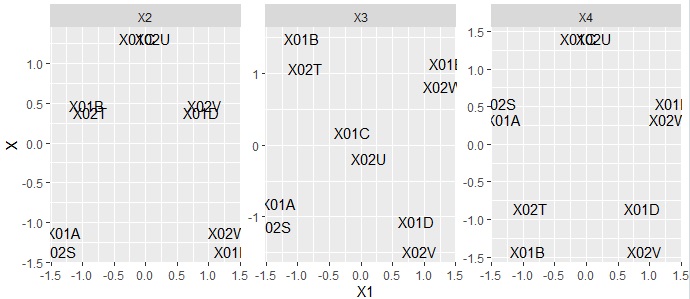
ちなみに、第１の変数の横軸にして、第２から、第４までの変数を縦軸にした散布図をそれぞれ作ると、下のようになります。
第１の変数は、想定している順番になる変数なのですが、それ以外の変数は違います。
ただ、変数の並び方を見ると、対称性があるので、モードの分解のような処理がされていることがわかります。
コレスポンデンス分析 のページで、コレスポンデンス分析と似た分析は、 主成分分析 でもできて、どちらかと言えば、主成分分析の方が万能のように書いています。
上記と同じ分析をを主成分分析で実行すると下図になります。
大体合ってはいるのですが、順番が正確に再現できていません。 このため、このページの方法としては、コレスポンデンス分析の方が良いようです。
上記の方法では、質的変数のグループを、そのグループの情報だけで連続変数に変換します。
これとは異なる方法として、目的変数の情報も使って、連続変数に変換する方法もあります。 広義の数量化Ⅱ類 に例があります。 ただ、目的変数と説明変数のグループの相関が高いのなら、目的自体を連続変数として使えば良いように思えるので、 筆者には使い道がよくわからないでいます。
「数量化理論とデータ処理」 林知己夫 著 朝倉書店 1982
数量化理論
のI 、Ⅱ、Ⅲ類について、フォートランを使った計算例が示されています。
このページの上記のような、各変数の散布図も示されています。
「一般化等質性分析による質的データのための尺度構成法」 土屋隆裕 著 土屋隆裕 1997
博士論文です。国立国会図書館のデジタルコレクションで一般公開もされています。
https://dl.ndl.go.jp/pid/3158293/1/1
提案されている手法が、一次元の尺度構成法で、順序データでもそうでなくても使えるようなので、
このページの方法と似た手法のようなのですが、筆者は詳細を読み取れていません。
順路
次は
標準化と正規化
