トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

２値変数のグループを、１つの連続変数に変換

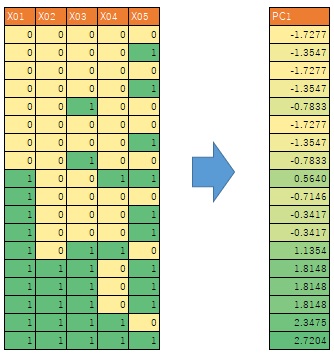
上の左側のデータは、0と1の２値だけになっています。 このページでは、こういう変数を「２値変数」と呼ぶことにします。 そして、右側のデータのように、小数点以下や負の値も含め、様々な数値が入っている場合を「連続変数」と呼ぶことにします。

質的データを量的データに変換 のページにあるように、２値変数は、質的データを表すことがあります。 質的な何かの「あり・なし」を表すのに、0と1を使っています。

２値変数のグループを変換して、連続変数を得る方法は、「尺度構成法」の一種です。 上の図の右側のデータは、尺度構成法を使って、左側のデータから得られたデータです。 質的データしか得ることができないような心理学関係の分野で、量的な分析を進めるための方法になっています。

２値変数がひとつだけだとできないのですが、複数あって、しかもそれらが共通の何かの影響を受けている場合に、 その何かを連続変数として得ることができます。 心理学関係では、「何か」というのが心理的な性質です。 テストのデータの場合は「英語力」のように、直接測ることが難しい尺度になります。

尺度構成法は、質的変数や２値変数でしか測定できないことを、あたかも連続変数で測定したように分析するための方法になります。 「温度」のような連続変数なら、１つの変数の測定で済みますが、尺度構成法では、複数の２値変数として測定して、連続変数の獲得につなげるところがポイントです。

項目反応理論と主成分分析

項目反応理論（IRT） と 主成分分析（PCA）は、いずれも、２値変数のグループを、１つの連続変数に変換する方法に使えます。

上の表のデータを２つの方法で比べると下図になります。 ほぼ一直線に並びますので、２つの方法には、ほとんど違いがないことがわかります。

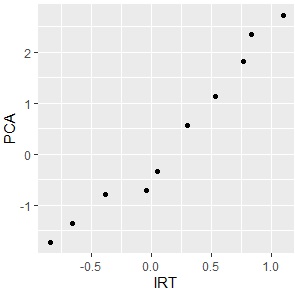
なお、この例では、１番目の因子同士を比べています。 ２番目の因子もあるようなデータでも、これらの方法は対応できます。

世の中の解説の中で、「 因子分析 と主成分分析は結果が似ている」と書かれているものを、時々見かけますが、それと同様のことが起きています。

項目反応理論と主成分分析で違いが出る場合

項目反応理論 には段階反応モデルというのがあり、順序尺度の場合も扱えます。

段階反応モデルでは、順序尺度は順序尺度として扱いますが、 主成分分析で、順序尺度の変数を扱う場合は、 ダミー変換 をして、順序の情報を失うか、順序尺度を連続尺度のようにして扱うかになって来るので、結果が似て来ないようです。

多次元尺度構成法

尺度構成法 のページに、広義と狭義の多次元尺度構成法の説明があります。

狭義の多次元尺度構成法は、 多次元尺度構成法のページにある内容で、 基本的に距離データを座標データ（連続データ）に変換する方法です。 例えば、都市間の距離のデータから、地図を作るための座標データを計算することができます。

そのため、元のデータを距離データに変換すれば、狭義の多次元尺度構成法も、上記のような1-0形式のデータの尺度構成法として使えます。

狭義の多次元尺度構成法を使う時の注意

まったく同じデータのサンプルがあると、それらのサンプル同士は、距離が０になります。 狭義の多次元尺度構成法のソフトウェアは、距離が０のサンプルがあるとエラーが出て、先に進めない場合があります。 1-0形式のデータの場合、連続データと違って、まったく同じサンプルが複数含まれることが起きやすく、実務的には不便です。

ちなみに狭義の多次元尺度構成法に限らず、 高次元を２次元に圧縮して可視化 にある他の方法でも、同様のエラーが起きることがあります。 Rの多次元尺度構成法やt-SNEではエラーが出て、できませんでした。

そのため、上記の項目反応理論と主成分分析の比較に、狭義の多次元尺度構成法との比較も加えようとしたのですが、 エラーが出るので断念しました。

手法の比較

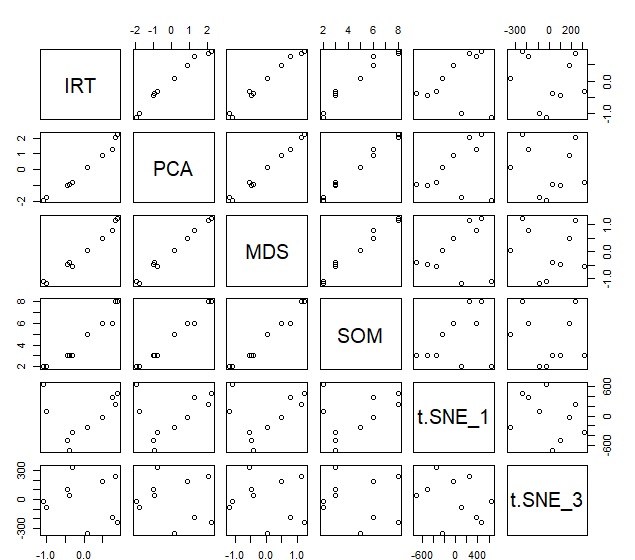
上記のデータセットから重複はなくしたデータセットを作って、各種の手法を比較しました。 ２次元に次元削減することが多い方法ですが、ここでは１次元に圧縮しています。

• IRT：項目反応理論
• PCA：主成分分析
• MDS：狭義の多次元尺度構成法の一種のsammon
• SOM：自己組織化マップ。格子は10個で、縦１列のみ
• t-SNE：t-SNE。添え字の1や3は、perplexity。dims=1に設定

IRT、PCA、MDS、SOMはほぼ同じ結果で、相関が高いです。t-SNEは、まったく相関がありませんでした。 t-SNEは、数字の傾向というより、各サンプルの近さだけを見る方法だからのようです。

２つ以上の連続変数にする使い方

上記では、２値変数のグループを、１つの連続変数に変換する話でした。 これだけが目的なら、２値変数の値について、サンプルごとに合計値や平均値を計算しても、１つの連続変数は作れますので、 わざわざ項目反応理論などを使わなくてもできます。

１つの連続変数だけを使う場合で、項目反応理論を使うのは、テストの問題の設計や分析もしたい場合が考えられます。

手法の比較は、１つの連続変数で用が足りる場合でしていますが、サンプルごとの合計値や平均値ではどうにもならず、尺度構成法が本当に威力を発揮するのは、 ２つ以上の連続変数でないと、うまくまとまらない場合です。

参考文献

「一般化等質性分析による質的データのための尺度構成法」　土屋隆裕　著　土屋隆裕　1997
博士論文です。国立国会図書館のデジタルコレクションで一般公開もされています。
https://dl.ndl.go.jp/pid/3158293/1/1
尺度構成法には、 ダミー変換したデータの主成分分析、 数量化�V類、 コレスポンデンス分析、 多次元尺度構成法 、 項目反応理論 などがありますが、結果が似ていたり、数学的には同じ手法になっていることを説明しています。

「多変量データ解析法　理論と応用」 柳井晴夫 著　朝倉書店　1994
主成分分析を、尺度構成の方法としても紹介しています。

「知覚・認知モデル論」 渡辺利夫　著　ナカニシヤ出版　2009
尺度構成の章があり、因子分析と項目反応理論が解説されています。

「データ解析　心理学研究法　１５」 東洋　著　東京大学出版会　1974
回帰分析、分散分析、判別分析、正準相関分析、因子分析、クラスター分析といった多変量解析の手法の章もありますが、 この本の特色は、0-1データの分析法にも、２つの章があることです。
・潜在構造分析：多数個の項目に対する反応を、少数のパラメータで解く方法。特色は、0-1型のデータを扱うこと。因子分析に近い。
・0-1データの相関は、四分相関や点相関。

順路 次は 質的変数のグループを、１つの連続変数に変換