ここでは、上のような分割表のデータを使います。
A-B型の中間層分析 のページでは、中間層分析の定義と、中間層分析でできることを説明しています。
このページは、中間層分析の種類の違いについてです。 以下では、 行列の分解（SVDやNMF）、 主成分分析、 コレスポンデンス分析 について比較してみたものです。
比較するためのデータは、分割表（頻度データ・カウントデータ）と、一般的な クロス集計 の２つにしてみました。
NMFは、3つの変数に圧縮しています。
Rのコードは、以下を使っています。
Rによる分割表のコレスポンデンス分析
Rによる行列の分解
Rによるクロス集計表の主成分分析
散布図は、 高次元を２次元に圧縮して可視化 をして作ったものです。
先にこのページの結論ですが、以下の３点です。
このページは、「分割表についてコレスポンデンス分析をする時に、よく行われているアプローチを他の方法でもやってみた。」というものです。
その方法のアルゴリズムが想定しないデータや、想定していないグラフの作り方をしています。 「想定外の使い方をすると、間違った分析結果になる」という例になっています。
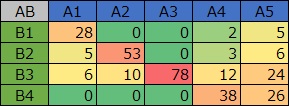
ここでは、上のような分割表のデータを使います。
変数の類似度の分析です。
左から順に、SVD、NMF、コレスポンデンス分析、主成分分析です。
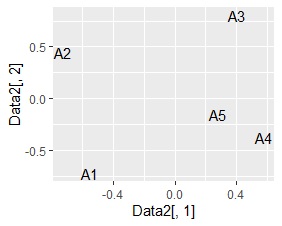
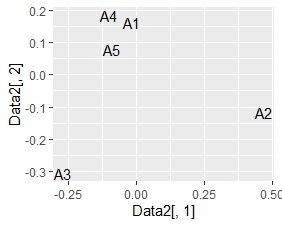
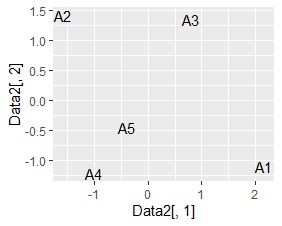
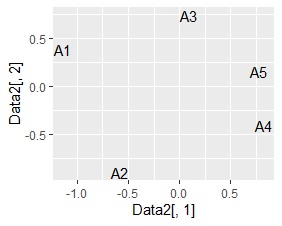
A4とA5が近く、A3とA5が近く、A1、A2がそれらから離れているようなデータですが、そうなったのは、SVD、コレスポンデンス分析、主成分分析でした。 NMFは、A1がA4とA5の近くに来ている理由がわかりません。
サンプルの類似度の分析です。
左から順に、SVD、NMF、コレスポンデンス分析、主成分分析です。
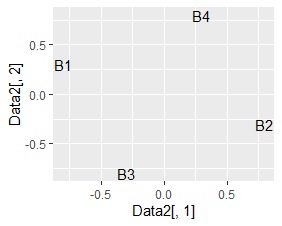
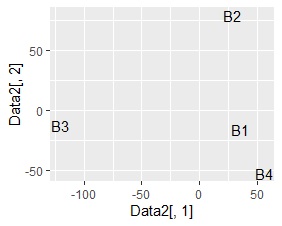
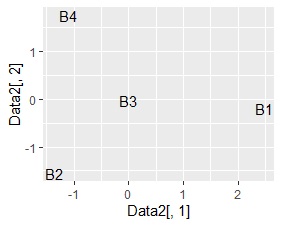
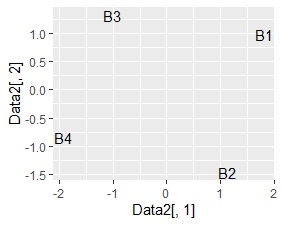
B3とB4が近づくことを期待しましたが、そうなったものはありませんでした。
多次元同時付置図による分析です。
左から順に、SVD、NMF、コレスポンデンス分析、主成分分析です。
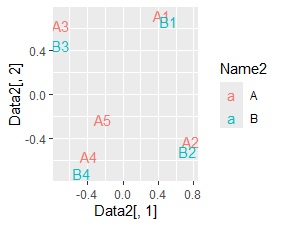
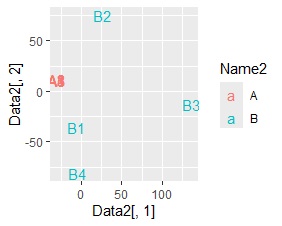
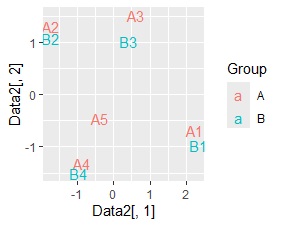
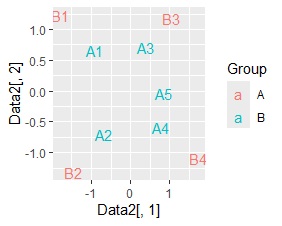
A1とB1、A2とB2、A3とB3、B4はA4とA5、B4は、A3とA5との間で値が大きいですが、値が大きいと近くに配置される特徴が、 SVDと、コレスポンデンス分析では出ました。
主成分分析は、SVDとコレスポンデンス分析の結果と似ていますが、AがBの内側に入るような配置になります。
NMFについては、AとBで値の範囲がかなり違い、同時付置図による分析に合っていないことがわかります。
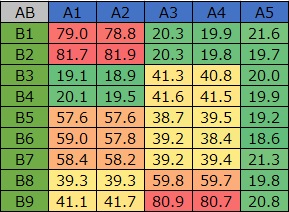
ここでは、上のようなデータを使います。
A1とA2、A3とA4の組合せについては、相関が高いです。 Bのグループについては、B1とB2、B3とB4、B5とB6とB7、B8とB9、という組合せについては、値が近いです。
NMFでは、３つの変数に圧縮しています。
左から順に、SVD、NMF、コレスポンデンス分析、主成分分析です。
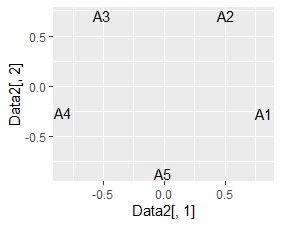
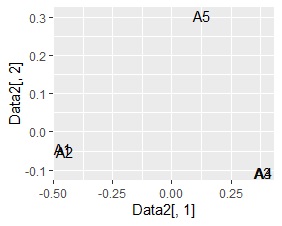
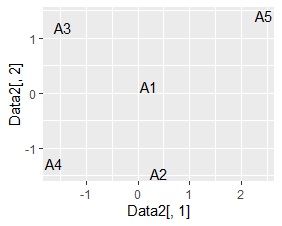
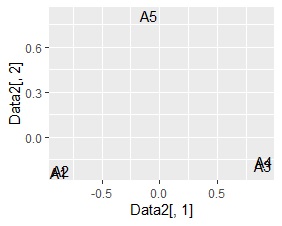
NMFと主成分分析は、相関が高い変数は近くに配置されました。
左から順に、SVD、NMF、コレスポンデンス分析、主成分分析です。
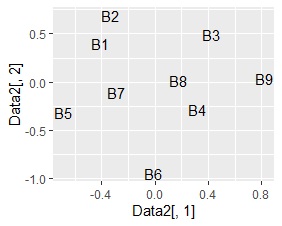
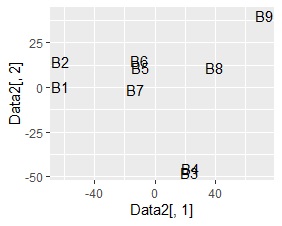
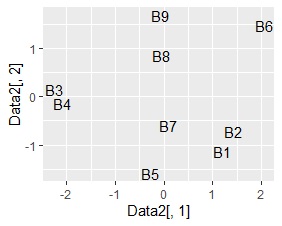
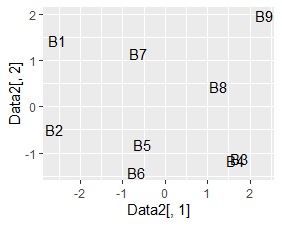
サンプルの値の近さがグラフに表れているのは、NMFでした。 主成分分析とコレスポンデンス分析は、NMFほどではないですが、サンプルの近さの特徴が出ていることがわかります。 SVDは、B8とB9の間にB4が来るなど、おかしな配置になりました。
左から順に、SVD、NMF、コレスポンデンス分析、主成分分析です。
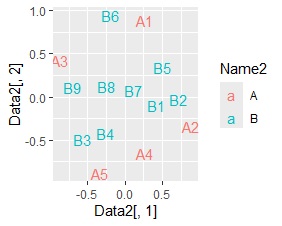
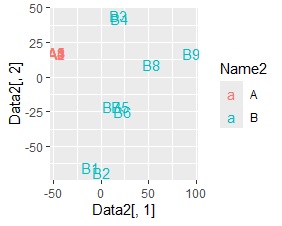
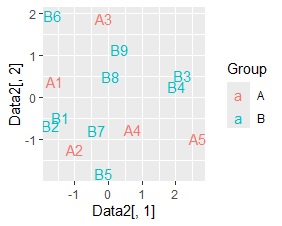
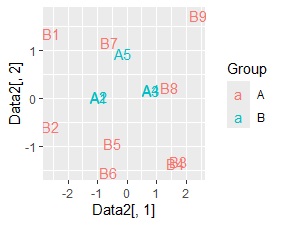
同時付置図は作れるのですが、どう解釈したら良いのかが、よくわからない図です。 コレスポンデンス分析の場合、A1、A2とB1、B2が近いので、値が特に大きいところの影響は出ているようです。
順路
次は
Q分析
