行列の分解
のページにあるSVDやNMFは、ひとつの行列を２つに分解する方法です。
分解された２つの行列を掛け合わせると、元の行列になるように分解されます。
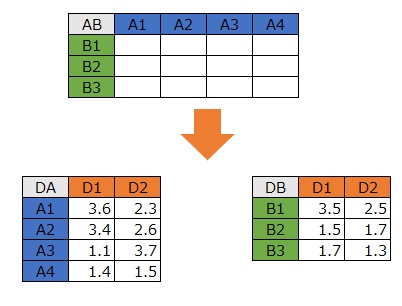
ところで、「分解された２つの行列を掛け合わせると、元の行列になる」という部分は成り立っていないけれども、 上のような分解をする方法は、他にもあります。
このページでは、そうした方法について、「中間層分析」という名前で呼んでおくことしています。
中間層分析には、以下のようなものがあります。
行列の分解の分解分析には、以下のようなものがあります。
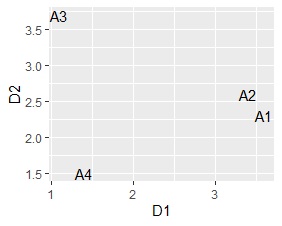
D1、D2という新しい変数を使って散布図を作ると、 変数の類似度の分析 ができます。
下のグラフでは、A1とA2が似ていることがわかります。
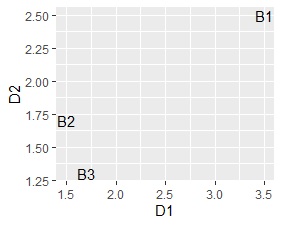
D1、D2という新しい変数を使って散布図を作ると、 サンプルの類似度の分析 ができます。
下のグラフでは、B2とB3が似ていることがわかります。
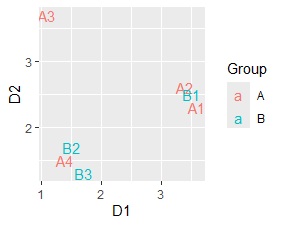
D1とD2という変数が共通していることを利用して、変数の類似度と、サンプルの類似度のグラフを重ね合わせることもできます。
行（変数）の項目と、列（サンプル）の項目の類似度の分析ができます。 多対多の分析 の一種の A-B型の分析 になります。
この分析に使われるのが、 同時付置図 です。
下の例では、A3が孤立していて、他は、２つのグループに分かれていることがわかります。
「Aの項目とBの項目の近さ」という考察を同時付置図でできるのは、 「分割表（頻度データ）の時」と「コレスポンデンス分析の時」です。 逆にいえば元のデータがどんな行列データでも良いわけではなく、また、主成分分析の時は使えないです。
この理由は、 中間層分析の使い分け のページにまとめました。
Rによる実施例は、 Rによる行列の分解 のページにあります。
順路
次は
同時付置図
