同時付置図

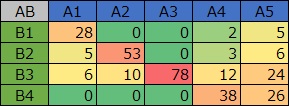
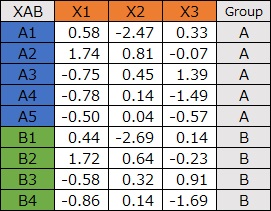
correspondence
同時付置図を使った分析をする時の元のデータは、左のようなものです。これについて、 A-B型の中間層分析をすると、右のデータを作れます。

上の例は、コレスポンデンス分析の場合です。

同時付置図は、このデータを散布図にしたものです。
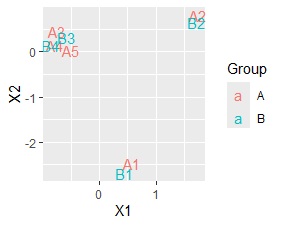
correspondence

同時付置図にすると、行と列の項目の近さを一緒に分析できます。

同時付置図の注意点

同時付置図は、とても便利なものですが、機械的に作って、「A1とB1は近い」といったような分析はできないです。ポイントは２つです。

同時付置図を作って、「A1とB1は近い」という考察ができるのは、分割表（頻度データ・カウントデータ）について、コレスポンデンス分析や行列の分解をした場合です。

主成分分析や、頻度データ以外でも同時付置図は作れますが、AとBの座標の意味が違うので、「A1とB1は近い」といった分析はできないです。

さらに、分割表について、コレスポンデンス分析や行列の分解をした場合だとしても、「A1とB1は近い」といった分析が難しい場合があります。

素直に、「A1とB1は近い」といった分析ができるのは、２つの変数だけに知りたい情報が入っている場合です。

上の例のように、X1、X2、X3という３つの変数が出て来ている場合は、X1とX2の散布図では、X3のことがわからないです。

下のように、変数の組合せごとに同時付置図を作って考察することはできますが、考察しにくいです。
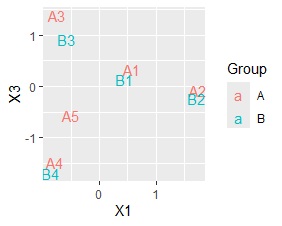
correspondence

この問題の解決策としては、多次元同時付置図があります。

Rの実施例は、 Rによる主成分分析の基本にあります。