上の３部グラフを作る時のデータを、２部グラフにすると、下のようになります。
多対多の分析 の内、 A-A型の分析 については、分析するための数理やグラフがけっこうあります。
一方、 A-B型の分析 については、数理はあるのですが、グラフは、多次元同時付置図によるコレスポンデンス分析 や ２部グラフ しかなく、これらだけでは数理で分析したことが見切れないことがあります。
なお、３部グラフというのは、A、B、Cの関係を見る方法です。 「３部グラフ」で検索してもなかなか記事は見つかりませんが、「Tripartite graph」で検索すれば、いろいろとあります。
多次元同時付置図によるコレスポンデンス分析 と、途中までが同じです。
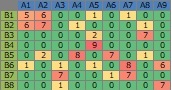
上の３部グラフを作る時のデータを、２部グラフにすると、下のようになります。
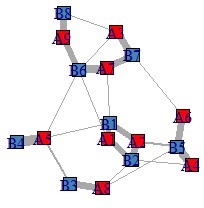
２部グラフ
を使うと、A-B型のデータの関係を直接的にネットワークグラフとしてみることができますが、「共通する要素がある」という考察がしにくいです。
上のデータに
コレスポンデンス分析
をします。
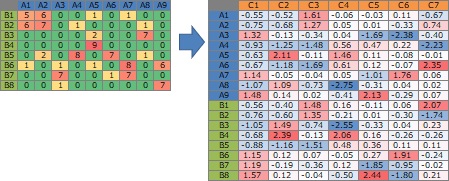
多次元同時付置図によるコレスポンデンス分析 では、コレスポンデンス分析で作ったデータを、多次元同時付置図にして分析します。
このデータを３部グラフにする方法としては、プラスとマイナスに分けて、絶対値の大きさで線を引くネットワークグラフが考えられます。
多次元同時付置図は、多次元になっているCを２次元に圧縮して対策しますが、
３部グラフでは、次元の数は残りますので、Cとの関係も見ることができます。
なお、下の３部グラフではCではなく、Xとなっています。
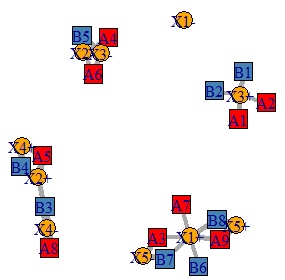
質的分割表のコレスポンデンス分析
と扱っているデータは同じですが、コレスポンデンス分析は使わないです。
まず、データを集計します。
次に、集計したデータを
ネットワークグラフ
の入力データにします。
Rの実施例は、 クロス集計表の３部グラフ のページにあります。
RPubsのページ
igprahで、３部グラフ（Tripartite graph）を描く方法が説明されています。
きれいな３部グラフができるのですが、紹介されている方法は、データの形がエッジリストになっていますし、特殊な記述方法をしています。
そのため、同時付置図用のデータを使うこのサイトの用途には合わないので、この方法は使っていません。
https://rpubs.com/barryrowlingson/tripartite
順路
次は
ISMとDEMATEL
