複雑なモデルの難しさ

複雑なモデルコンピュータの能力がどんどん上がって来た事もあり、多変量解析のいろいろなものが、実務の場で使えるようになっています。

多変量解析には、いろいろなものがありますが、多変量の関係が複雑なものの表現の仕方は、大きく２つに分かれます。

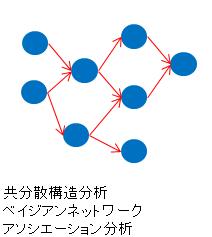
ひとつは、それぞれの変数同士が複雑なつながりを持っている事を表現したモデルです。共分散構造分析、ベイジアンネットワーク、アソシエーション分析などがあります。

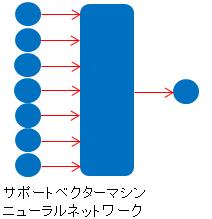
もうひとつは、たくさんの説明変数の合成が、目的変数とつながっている事を表現したモデルです。サポートベクターマシンや、ニューラルネットワークなどがあります。

複雑なモデルを使う時の難しさ

「コンピュータが自動的に状況をモデルにし、意思決定する時代が来た」、と思いたくなりますが、そうでもありません。

相関係数で見える事と見えない事、過学習、外挿、外れ値、欠損値、といったものが、データ解析の注意点や難しさとして、昔からあります。モデルが複雑になって来ると、昔からの話も複雑に絡んで来ます。

データとソフトとコンピュータを用意すれば、わりと簡単に計算結果を出せる時代になりましたが、実務に使える結果には、程遠い事がよくあります。

複雑なモデルは、落とし穴の場所も複雑になって来るので、実務では、扱いに困る事がよくあります。

ただ、「実務に使える結果には程遠い」、と言っても、欲しい結果に行き着くための、ヒントになる事があります。

単純なモデルや、グラフによるデータの可視化も合わせ、また、時にはデータそのものをよく観察して、解析の目的をやりとげるのが、今のところ現実的な方法のようです。

本当は、すべての落とし穴に対して、万全の対策をしたソフトが、登場すれば良いのですが、、、
いつになるのかはわかりませんので、筆者の場合は、とりあえず、このような使い方をしています。

このページでは、冒頭に複雑なモデルの２系統を書きました。これらの両方の特徴を持つモデルも思い付く事ができますが、そんなモデルの前に、考えなければいけない事がいろいろあるようです。