トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
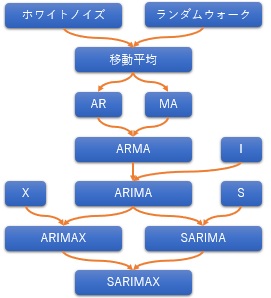
時系列分析 の比較的古い文献では、ARMAモデルが説明されることが多いです。 その後、ARIMAの紹介が増えて、最近は、ARIMAXやSARIMAが説明されることが増えました。 今のところ、最大のモデルはSARIMAXのようです。
SARIMAXは、S、AR、I、MA、Xのモデルの足し合わせでできているので、個々のモデルを理解する必要があります。
世の中の解説では、「ARIMA」、「SARIMA]、「ARIMAX」といった感じで、要素を合体した名前で呼んで解説しますが、要素で分けた方がわかりやすいので、ここでは、要素別に説明します。
ARとMAは、既に説明しているので、S、I、Xを順に説明します。
Iモデルの「I」は、「Integrated：和分」ですが、実際の作業は、差分を扱います。
上記で、ランダムウォークモデルのシンプルな式として、以下を考えました。
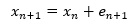
ここで、以下のようにyを考えます。
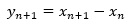
すると、yの予測式はシンプルです。
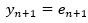
元のデータでは、うまく当てはまるモデルが見つからなくても、 差分を分析対象にすると、モデルが当てはまることがあります。
例えば、位置データの差分は、移動距離を表します。 温度の差分は、熱エネルギーに比例します。 差分は、当てはまりを良くするための、単なる計算テクニックではなく、物理現象の分析として、意味のある分析になっていることもあります。
データが直線的な上昇や下降をしている場合、つまり、トレンドを持っている場合、差分を取ると、トレンドに分を除いた情報が見やすくなります。
Iモデルは、トレンド（非定常性の一種）を扱う方法として紹介されることが多いです。
Sモデルの「S」は、「Seasonal：季節性の」から来ていますが、季節性に限らず、１週間でも、１日でも、周期性があれば扱えるモデルです。
まず、ランダムウォークモデルとして、以下を考えます。
これは、予測値を１ステップ前の値と考える式になっています。
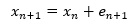
Sモデルのシンプルな式は、例えば以下になります。
１か月に１個データがあり、12か月ごとの周期的な変化のあるデータの場合に当てはまる式です。
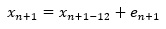
時系列分析の方法にProphetがありますが、Prophetでは、周期性を三角関数で扱います。 三角関数の場合は、過去にわたってずっと同じように周期的な変化をしている場合に向いています。
Sモデルの場合は、例えば、上の例では12か月前のデータしか参照していないので、「周期性はあるが、長い年月の中では周期的な特徴が変わって来ている」という場合も扱えます。
Iモデルは、隣接したサンプルとの差分を扱います。 さらに、一般化して、差分の差分、差分の差分の差分、といった形で、数学的な性質が研究されています。
Sモデルの数学的な扱い方を説明している文献では、隣接したサンプルではなく、「１周期前のサンプルとの差分」というようにして、Iモデルの理論が応用されています、
Xモデルの「X」は、「exogenous：外生の」です。
単回帰分析
は、以下のような直線を表す式のモデルです。
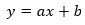
単回帰分析を正確に表現する式は、以下になります。
eは誤差です。
実際のデータは、直線状ではなく、直線からばらつきますが、eがばらつきの分を受け持つことで、実際のデータを表す式になります。
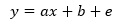
データとの対応を、より正確に表す式が以下になります。
これは、n+1番目のサンプルに対して成り立つ式ですが、任意のサンプルのことも表しています。
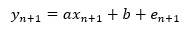
前置きが長くなりましたが、シンプルなXモデルは以下になります。
ここまで説明して来た、ホワイトノイズモデルからIモデルまでは、使用する変数がxだけでした。
Xモデルでは、別の変数が加わるところが、大きな違いです。
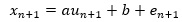
Xモデルは、過去のデータとは関係なく、aやbが求まるので、単体では時系列分析のモデルではありません。 他のモデルと組み合わせると、時系列分析のモデルになります。
S、AR、I、MA、Xの組み合わせ方で、呼ばれることもあります。
元のデータについて、差分を計算して、その差分についてARMAモデルを作ると、それはARIMAモデルになります。
ARIMAモデルの理論式は、もっと高度ですが、実務では、この処理で足りることが多いです。
元のデータについて、一周期前のデータとの差分を計算して、その差分についてARMAモデルを作ると、それはSARIMAモデルになります。
SARIMAモデルは、１周期前のデータを変数として加えたARIMAモデルでも、SARIMAモデルになります。
SARIMAモデルには、乗法型と加法型があります。 乗法型は、Iモデルによる隣接との差分を取る処理と、Sモデルによる周期の差分の掛け算（乗法）でできています。 加法型は、トレンド、季節性、誤差の項の和でできているモデルです。 ちなみに、Prophet や SARIMAXTモデル は加法型の一種です。 三重指数平滑法 には、加法型と乗法型があります。
ARモデルで１周期前も含むサイズにすると、季節性を考慮しています。 違いは、 周期性とARモデルの関係 のページで説明しています。
ARIMAモデルに、外生変数の項を加えると、ARIMAXモデルになります。
SARIMAXモデルは、このページで説明した部品をすべて盛り込んだモデルです。
「経済の時系列分析 」 山本拓 著 創文社 1988
トレンドを除く方法として、ARIMAモデルを紹介しています。
元のデータが、定常になっている変数の和分になることから、Iモデルの「Integrated：和分」という呼び方になっている。
加法型と乗法型のSARIMAモデルが解説されています
「現代時系列分析」 田中勝人 著 岩波書店 2006
AR(1)モデルによって、トレンドを持つデータのモデルとして、ARIMAモデルを紹介しています。
乗法型のSARIMAモデルが解説されています。
順路
次は
MAレスSARIMAXモデル
