GARCHモデルは、ARMAかESか

以下は、筆者の私見です。誤解があれば、ご教示いただけると幸いです。

ARCHモデルは、ARかMAかと似たことが、GARCHモデルにもあります。 GARCHモデルの場合は、「ARMAかES（指数平滑モデル）か」です。

GARCHモデルは、「 ARMAモデルと似ている」と説明する文献と、「指数平滑モデルと似ている」と説明する文献があります。

どちらも正しいです。

GARCHモデルは、式の形がARMAモデルと似ている

GARCHモデルは、以下の式になっています。

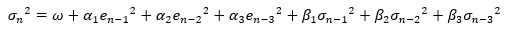
この式の右辺の中で、左半分はARCHモデルと同じです。 ARCHモデルは、ARかMAかのページで、ARCHモデルがMAモデルと似ているとする理由と同じで、GARCHモデルのARCHモデルの部分は、MAモデルと似ています。

右半分はGARCHモデルで追加された部分ですが、左辺にn番目のσがあって、それを過去のσで推定する形になっているので、ARモデルと似ています。

このように解釈すると、GARCHモデルは、以下の ARMAモデルの式と似ています。

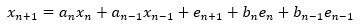
このように考えると、ARMAモデルのために作られた理論が、GARCHモデルに使えることになります。実際、そのようにして進められた研究も見かけます。

ただ、一見すると似ているのですが、実は大きな違いがあります。それは、ARMAモデルのxが観測値なことに対して、GARCHモデルがσは統計量なことです。

そのため、ARMAモデルの理論が適用できない場合もありそうです。適用する時は、その点への配慮が必要ですが、既存の研究でどこまで配慮されているのかまでは、筆者は調べたことがないです。

MAモデル単体の場合は、想定されているxが、観測値でもあり統計量でもあるので、 ARCHモデルは、ARかMAかでは、この違いについて説明していません。 ARMAモデルになると、xが統計量ではなくなるので、この違いがあります。

指数平滑モデルは、以下の式になっています。
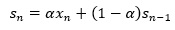
単純指数平滑法

上のように、eを過去３つ、σを過去３つ参照するGARCHモデルは、GARCH(3,3)と言いますが、指数平滑モデルは、GARCH(1,1)と似ています。

指数平滑モデルのsは、統計量です。その点では、GARCHモデルは、ARMAモデルよりも、指数平滑モデルの方が似ています。