 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
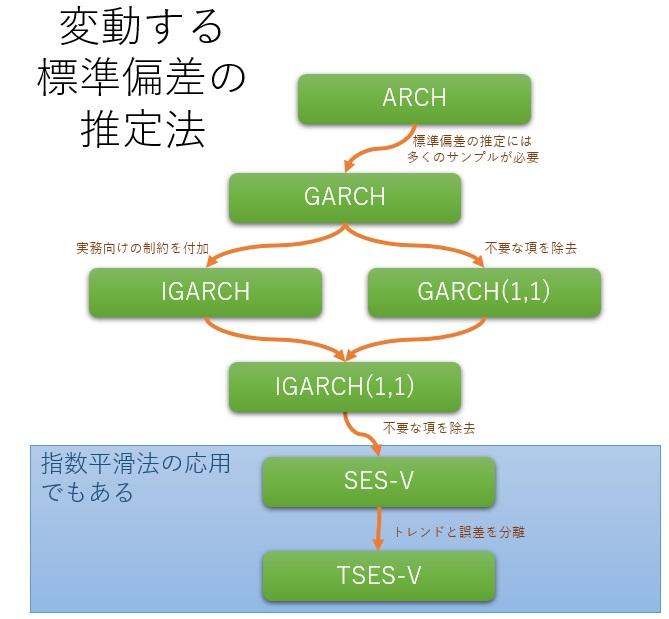
株価が典型的ですが、金融関係の 時系列分析 では、価格の変動を見ます。
価格の変動は、
ランダムウォークモデル
と似ていることが知られています。
ランダムウォークモデルは、以下のような式です。
1ステップ前の値に乱数を足したものが、次の値になっていることを表します。
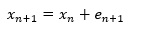
ここで、以下のようにyを考えると、yの式は乱数だけを表します。
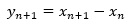
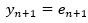
eとしては、例えば、「平均値が0で、標準偏差が100の正規分布」というように考えることが普通です。
ところで、「標準偏差が100」と考える時には、暗黙のうちに、「ばらつきは一定」ということを想定しています。
一方、金融関係では、ばらつきが変化している現象が指摘されています。
ばらつきが大きい時期の投資はリスクが大きくなるので、ばらつきの大きさを把握しておく必要があります。
ボラティリティというのは、ばらつきのことですが、ボラティリティのモデルでは、扱い方に特徴があります。
上記のeを、σ(シグマ)とε(イプシロン)の積で考えます。
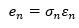
添え字のnは、n番目のサンプルの値であることを表します。 ボラティリティは、σです。 εは、標準偏差が1の分布です。
eのデータは、例えば、-1,3,7,-5,-2,2,8,-3、というように、ばらばらに大きさが変化します。 ボラティリティが一定の場合は、これらの標準偏差がばらつきを表します。
σとεの積にすると、 「ボラティリティの変化を表現するのがσ、ばらばらな変化を表現するのがε」として、役割を分けることができるようになります。
ボラティリティの時系列分析では、σの値を推定します。
以下では、順に方法を説明します。
移動平均モデル は、ボラティリティの推定でも作れます。
例えば、直近の3つのデータで推定するのなら、以下の式です。
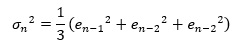
ARCHモデルは ARモデル と似ていて、移動平均モデルを一般化したものです。
例えば、直近の3つのデータで推定するのなら、以下の式です。
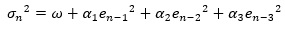
ARCHモデルの解釈として、 ARCHモデルは、ARかMAか のページがあります。
GARCHモデルは、ARCHモデルを改良したものです。
例えば、直近の3つのデータで推定するのなら、以下の式です。
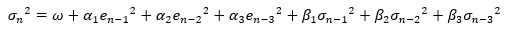
GARCHモデルは、過去のσも参照する式になっています。 上の式は直近の3つのデータを使うものですが、 過去のσの推定する時には、さらに過去のデータが入っているので、結果的に、GARCHモデルには、過去の多くのデータを参照するモデルになっています。
ホワイトノイズからSARIMAXまでの道のり のページでは、データの平均値を推定しています。 平均値を推定する時は、直近の数個のデータでも、そこそこの精度の予測になります。 ところが、 誤差とn数 のページにあるように、標準偏差の推定では、少なくとも数十個はないと、安定した推定ができません。
そのため、上の例は、3個でARCHモデルを作りましたが、少なくとも数十個の項があるARCHモデルを作る必要があります。 巨大なモデルになってしまいます。
ここでひとつポイントがあり、ボラティリティの変化を想定しているので、直近のデータほど重みをつけたARCHモデルの方が良いです。
GARCHモデルにすると、少ない項でも、過去の多くのデータを含めることができ、しかも、直近のデータほど重みがつきます。
GARCHモデルの解釈として、 GARCHモデルは、ARMAかETSか のページがあります。
上のGARCHモデルは、過去の3つのデータを使うようになっています。 GARCH(3,3)と表現します。
ところで、GARCHモデルは、過去の多くのデータを含むようになっているので、もっと簡略にしても、精度がほとんど変わらないです。
αとβが1個ずつしかない、GARCHモデルは、GARCH(1,1)と呼ばれています。
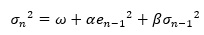
直近3つのデータを使うARCHモデルでは、「精度が悪い」となるのですが、GARCHモデルの場合は、直近1つのデータでも「実用的」となります。
GARCHモデルについて、係数の和に「1」という条件を付けたモデルは、「IGARCH」と呼ばれています。
例えば、上のGARCHモデルの場合は、条件が以下のようになります。
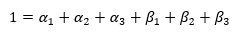
1よりも大きいと発散傾向、1よりも小さいと収束傾向になります。 ちょうど1の時は、ボラティリティの変動を表しやすいです。
「GARCHモデルは、GARCH(1,1)で十分」という話は、IGARCHについても同様なので、IGARCH(1,1)がベストです。
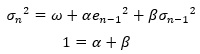
以下の書き方でもできます。
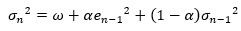
ここまで、「ω(オメガ)」という項については、触れませんでしたが、ARCHやGARCHでは、ωが入っています。
GACRHモデルは、過去の推定値を参照するので、ωが入れ子のようにして、式に含まれています。 n=1からn=2に進む時に、ωが含まれます。 n=2からn=3に進む時には、(1+β)ωが含まれます。 n=3からn=4に進む時には、(1+β)(1+β)ωが含まれます。 このようにして、nが増えるごとにωの影響が増大するようになっています。
これが成り立つのは、ボラティリティが一定値に収束する場合か、ωが0の場合です。
ところで、ωがなかったとしても、ボラティリティが一定値に収束することは分析できるます。 そう考えると、ωは不要です。
前項までで、「ボラティリティのモデルはIGARCH(1,1)がベスト」となっていましたので、ωの事も含めると、結論としては、以下がベストになります。
係数がαの1個しかない非常にシンプルな式ですが、ここまでで説明したように、これで十分です。
このモデルは、「EWMAモデル」と呼ばれます。
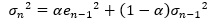
ちなみに、筆者は、GARCHモデルで計算すると、ωがほぼ0になることが多いことから、「そもそもωは不要では?」と気付きました。
ωが付いているので、GARCHモデルとEWMAモデルを比べると、GARCHモデルの方が、分析ができることが増えるように見えます。 しかし、ωが0以外のケースは、かなり特殊なケースなので、実はそうでもないのが、面白いところです。
EWMAは、「Exponentially Weighted Moving Average:指数重み付き移動平均」の略です。 日本語では、 指数平滑法 (Exponential Smoothing:ES) と呼ばれている方法の別名です。
指数平滑法は、平均値を推定する方法として説明されることが一般的ですが、ここではボラティリティの推定の式になっています。
共分散の逐次学習 の式と、似ています。
いわゆる逐次学習は、真の値が一定なことを想定しています。 EWMAモデルは、真の値が変化することを想定しています。 その違いが、係数の違いになっています。
EWMAモデルは、パラメータがαしかありません。 αしかないということは、計算が楽になることが利点のひとつです。
αを使うことで、ボラティリティの安定性が分析できるようになります。 EWMAモデルは、この点が優れています。
αが1の時は、ボラティリティが常に変動していて、非常に不安定です。 αが0の時は、ボラティリティが変化しないことを表します。
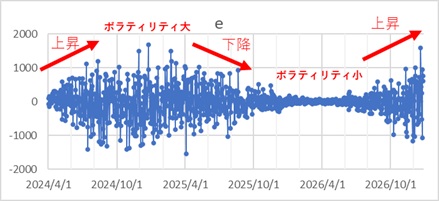
まず、下がばらつきを表すeのグラフです。

上のデータについて、ボラティリティのσを推定した結果が下のグラフになります。 αが0.01と0.1の場合です。
普通は、ボラティリティσがわからないので、モデルを使って推定するのですが、 この例で使っているeは、人工的に作成したものなので、σの真値がわかっています。 真値がわかれば、推定の正しさがわかります。
下のグラフでは、σの真値も併記することで、答え合わせをしています。
αが0.01でも、0.1でも真値と似ているので、EWMAモデルが大きく間違った推定をしていないことがわかります。
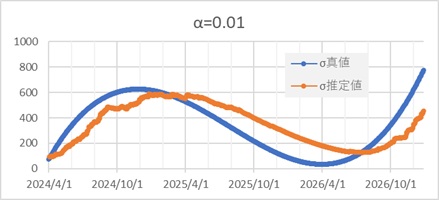
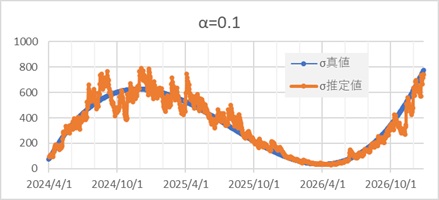
αが0.01の時は、滑らかなカーブに近くなり、その点は良いです。 しかし、過去の値の影響を受けやすいので、σの変化への対応が遅れています。
αが0.1の時は、変化対応への遅れがあまりない点が良いです。 しかし、滑らかなカーブではなくなっています。
滑らかなカーブと遅れがない事を両立するための方法としては、αが0.1の結果について、近似曲線を使う方法があります。
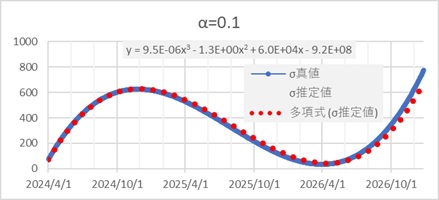
この例の場合は、σの真値が3次曲線なので、3次曲線できれいな近似ができます。
近似曲線がうまく作れれば、未来の値を計算することもできるようになります。
上記の実施例は、Excelで作っています。 EWMAモデルなら、EXCELで簡単に扱えます。
Excelでボラティリティ推定モデル で、具体的な手順を説明しています。
「フィナンシャルリスクマネジメント」 ジョン・C.ハル 著 ピアソン・エデュケーション 2008
ARCH、EWMA、GARCHの順で説明しています。
筆者が調べた限りでは、EWMAを紹介している日本語の本は、この本だけです。
この本では、GARCH(1,1)の方が、EWMAよりも理論的な魅力があるものとして説明されています。
「実証のための計量時系列分析」 ウォルター・エンダース 著 有斐閣 2019
ARCH、GARCH、IGARCHなどを紹介しています。
順路


 次は
トレンド修正付きボラティリティ推定モデル
次は
トレンド修正付きボラティリティ推定モデル

