以下は、筆者の私見です。 誤解があれば、ご教示いただけると幸いです。
SARIMAX 、 三重指数平滑法 、 Prophet など、時系列分析の代表的なモデルは、平均値の変化を扱うモデルです。 ボラティリティモデル は、標準偏差の変化を扱うモデルです。 ARCHモデル は、ボラティリティモデルのひとつです。
ARCHモデルは、名前に「AR」と入っていますが、「Auto Regressive」の略なので、この点は ARモデル と同じです。
面白いことに、ARCHモデルは、「 ARモデル と似ている」と説明する文献と、「 MAモデル と似ている」と説明する文献があります。
以下で、理由を説明しますが、結論としては、どちらも正しいです。 乗法型のARモデルと似ていて、かつ、MAモデルと似ています。
ARCHモデルでは、誤差eを、σ（シグマ）とε（イプシロン）の積で考えます。
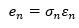
そして、σを過去のeを使って推定します。
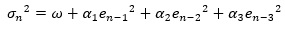
ARCHモデルの２つの式をまとめると、以下になります。
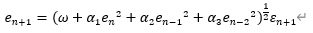
未来のeを、過去のeと、未来のεで予測する式になっています。
「未来のeを、過去のeと、未来のεで予測する式になっています。」という説明文について、 「e → x」、「ε → e」というように入れ替えると、ARモデルの説明文と同じになります。 この意味でARCHモデルとARモデルは似ています。
ただし、ARCHモデルは乗法型、ARモデルは加法型という違いがあります。
以下のように考えることで、ARCHモデルが加法型でも、「ARCHモデルは、ARモデルの式になっている」とする説明の仕方が、世の中では一般的のようです。
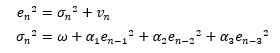
２つの式をまとめると、以下のようになります。
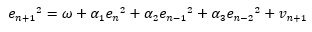
こうすると、加法型のARモデルと式の形が似ています。 そのため、もっともらしく見えますが、不自然なところが２つあります。
まず、ボラティリティの変化に応じて、vの分布の範囲が変わるので、vに正規分布や一様分布のような分布を仮定できなくなります。
また、
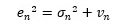
という式は、左辺が二乗した値なので、両辺は正の値になることを意味しています。
このため、vは、ボラティリティσの二乗のマイナスの値よりも大きいことになります。
不自然な性質を持ったモデルです。
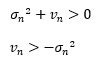
以上のようになっているので、ARCHモデルとARモデルの類似性は、加法型よりも乗法型で説明した方が良いと筆者は考えています。
MAモデルでは、式が、例えば以下のようになります。
n+1番目のxは、定数のc、乱数e、係数bで求まる式です。
２乗かどうかの違いがありますが、MAモデルとARCHモデルは、式の形が似ています。
なお、「MAモデルと似ている」という時の見方は、 GARCHモデルは、ARMAかESか で、「ARMAモデルと似ている」という時にも使います。
