指数平滑法

指数平滑法は、移動平均モデルの発展型です。

指数平滑法では、重みを付ける時に、入れ子のようにすることで、指数的な重みの付け方で、直近のデータほど重視するように重み付けします。

ちなみに、移動平均モデルに重みを付ける他の方法としては、 ARモデルもあります。

指数平滑法の式

指数平滑法は、以下の式を使います。この式は、局所的な平均値を求める式になっています。
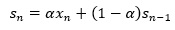
単純指数平滑法

ARモデルと同様の書き方をするのなら、予測式は以下になります。
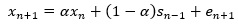
単純指数平滑法

αは０から１の間にしますた、 αが０の時は、ホワイトノイズモデルと同じです。 αが１の時は、ランダムウォークモデルと同じです。そのため、単純指数平滑法は、両極端にホワイトノイズモデルとランダムウォークモデルを持った中間モデルです。

ARモデルは、いくつ前のサンプルまでを参照するのかや、そのサンプルの係数の大きさを個別に調整しますが、単純指数平滑法は、「直近のサンプルほど重視する」という考え方で、そこに指数の方法を使います。計算が軽くなり、実務向きな手法になっています。

単純指数平滑法は、平均値の逐次学習の式と、似ています。

いわゆる逐次学習は、真の値が一定なことを想定しています。単純指数平滑法は、真の値が変化することを想定しています。その違いが、係数の違いになっています。

一般的な文献では、「指数平滑法」と言っている時は、上記の式のことです。 Excelでも、「指数平滑法」は、上記の式のことです。

三重指数平滑法も解説している文献では、上記の式の場合を、「単純指数平滑法」と呼ぶことがあります。

指数平滑法の英語名は、「Exponential Smoothing」です。ソフトの関数名では、「ES」となっていることがあります。英語の略称には、「EWMA」もあります。これは、「Exponentially Weighted Moving Average：指数重み付き移動平均」の略です。

指数平滑法には、上記の式を発展させたものとして、三重指数平滑法があります。

また、一般的な指数平滑法は、局所的な平均値を求める方法ですが、応用として、局所的な標準偏差を求める方法も知られています。これは、 EWMAモデルと呼ばれています。