 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
ボラティリティ推定モデル のページでは、文献で見かけるボラティリティの推定方法と、その改良版としての EWMAモデルを説明しています。
先行研究で、すでに指摘されているかもしれませんが、 ボラティリティ推定モデル のページの方法では、「トレンドに対応していない」という不備があります。
車輪の再発明かもしれませんが、筆者が独自に修正方法を考えたので、このページで説明します。
タイトルに「トレンド修正付きボラティリティ推定モデル」とありますが、具体的な名前は、「TEWMAモデル」です。 「EWMA」に、トレンド(Trend)のTを付けました。
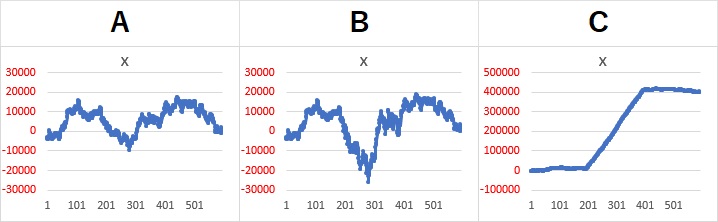
以下のような、A、B、Cの3つのパターンを例にします。価格変動をイメージした例です。 A、B、Cは、1〜200番目と、401〜600番目のデータがまったく同じです。 Aについて、201〜400番目のデータを加工して、BとCを作っています。
AとBの201〜400番目は、振れ幅が違うように見えます。
Cは、201〜400番目のトレンドが強いので、AやBとは見た目が大きく異なりますが、1〜200番目と、401〜600番目のデータは同じです。
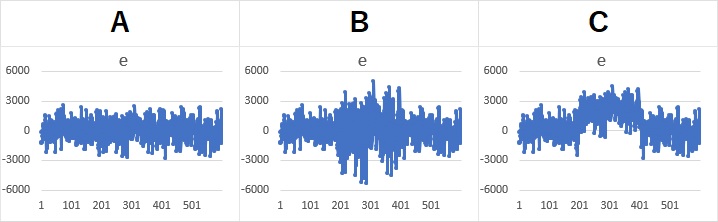
上のデータについて、前後のデータの差を計算すると、 ボラティリティ推定モデル のeになります。
eを見ると、Bの201〜400番目は、ばらつきが2倍くらいになっていることがわかります。
Cの201〜400番目は、ばらつきは変化していないようですが、0を中心としたばらつきではなく、上側に偏っています。
上側に偏ることが、トレンドとして表れていることもわかります。
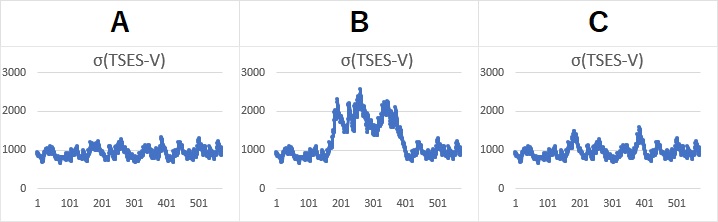
上のデータについて、
ボラティリティ推定モデル
で、ボラティリティσを計算すると、以下になります。
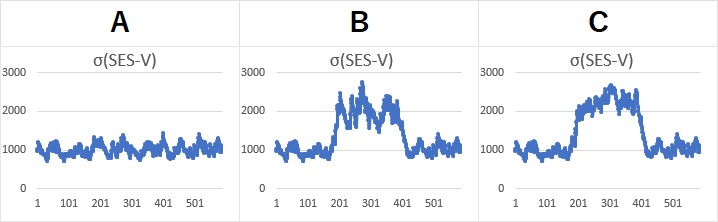
Aは、σが約1000で一定らしいことがわかります。 BとCは、「1000 → 2000 → 1000」と変化していることがわかります。 つまり、BとCの違いが、ボラティリティではわからなくなっています。
「ボラティリティはばらつき」と考えるのが普通なので、Bの計算結果は正しいです。 Cの計算は、計算方法に不備があることがわかります。
このページでは、Cの場合も正しく計算できる方法を説明します。
ボラティリティの推定では、eをそのままではなく、eの2乗を使います。
そのため、例えば、0を中心にして、ばらついている場合と、その時のマイナス側のデータを全部プラスに変換した場合では、ボラティリティが同じになります。
そのため、BとCのような違いがあったとしても、ボラティリティの値が似てくることが起きます。
トレンドがあると、eの中心が0ではなくなるのですが、上の計算では、その点が考慮されていません。
中心の位置が考慮できていないことが原因なので、考慮するように式を作ります。
EWMAとTEWMAを比較すると以下のようになります。
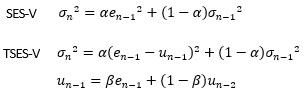
EWMAのeのところを、中心値の推定値を引くことで、TEWMAでは修正しています。
中心値の推定値の計算は、この例と異なっても良いのですが、EWMAが指数平滑法なので、ここでは平均値の推定も指数平滑法にしています。
指数平滑法以外としては、近似曲線なので、中心値を推定することもできます。
TEWMAで計算すると、以下のようになります。
Cは対策ができています。
トレンドがないAとBがEWMAとあまり変わらないのは、狙い通りです。
TEWMAモデルもEWMAと同様に、EXCELで簡単に扱えます。
Excelでボラティリティ推定モデル で、具体的な手順を説明しています。
TEWMAモデルは、母平均と母分散が変化していることを仮定して、それらをデータから推定するための推定モデルです。
このデータができることを説明している発生モデルは、 母数変動型ランダムウォークモデル になります。
順路


 次は
移動分析
次は
移動分析

