トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
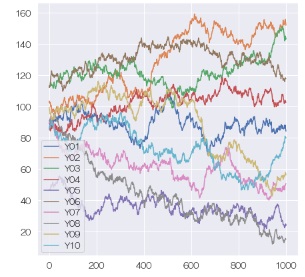
ランダムウォークモデル
のページでは、一見、まったく違う現象に見えていても、モデル式が同じになるケースとしてランダムウォークモデルを説明しています。
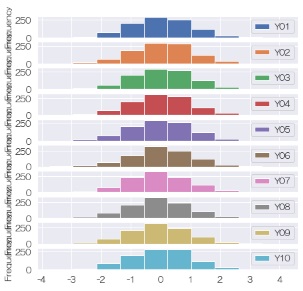
さらに、右のヒストグラムを示して、差分の分布が同じであることを説明しています。
上の例の場合は、差分の分布が、母平均が０・母分散が１の正規分布です。
ランダムウォークモデルは、以下のようになります。
eの部分が差分になります。
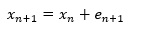
ランダムウォークモデルは、これだけでも興味深く、株価の動きのモデルとして説明されることもあります。
ところで、上記の説明では、暗黙のうちに、「母平均が０で一定、母分散が一定の正規分布」と仮定しています。 上記の例では、その仮定で問題がないのですが、そうではない可能性として２つあります。
ひとつは、「正規分布」ではない場合です。 正規分布ではない場合としては、1と-1の二値の場合を、よく見かけます。
もうひとつは、「母数（母平均と母分散）が一定」という仮定がない場合です。 以下では、この場合について、説明します。
母数変動型ランダムウォークモデルとしては、母平均が変動する場合、母分散が変動する場合、両方が変動する場合があります。
下の例では、母平均が０からだんだん増えて行き、29番目のサンプルでピークになります。 その後、だんだん減って、０を通り過ぎて、58番目のサンプルからマイナスになります。
母分散は、１で一定です。
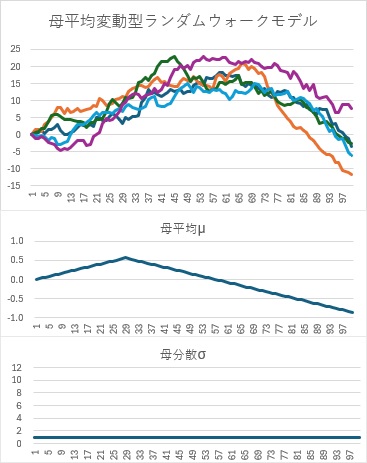
母平均がプラスの時は、５つの線がどれも、上昇傾向のトレンドを持っています。 また、マイナスの時は、下降傾向のトレンドを持っています。
母平均が０のランダムウォークモデルでも、一部の線だけが上昇や下降のトレンドを持つことはあります。 全部がトレンドを持つ可能性はありますが、非常に稀です。
ところが、母平均が０ではなくなると、当たり前のようにして、全部が同じトレンドになります。
金融関係の時系列分析では、価格変動のばらつき方（ボラティリティ）が時期によって異なることが知られていて、 ボラティリティ推定モデル が研究されています。
文献によっては、「ARCH過程」や「GARCH過程」と呼んで、 ボラティリティ推定モデル 自体を現象のモデルのように説明することがあります。 しかし、筆者は、ARCHやGARCHは、あくまで母分散を推定するためのモデルであり、現象のモデルとしては、母分散変動型のランダムウォークモデルを想定した方が良いように考えています。
以下は、母平均が０で一定です。母分散は、50番目のサンプルでピークになる形で、増減しています。
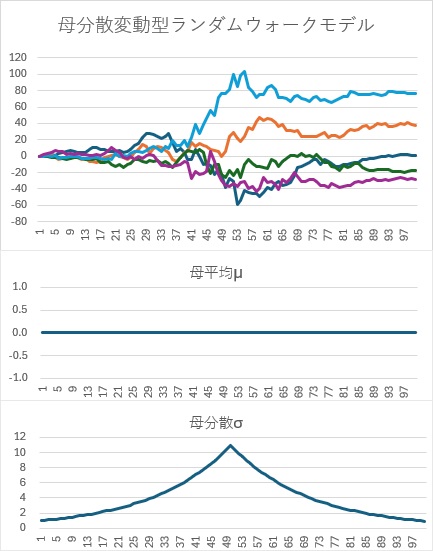
母分散が大きくなると、動きが大きくなります。 母分散が小さい時も、動きはありますが、相対的に小さいので、一定のようにも見えます。
母平均と母分散の両方が変動する場合、さらに複雑になります。
複数が同じトレンドを持っている時は、母平均がプラス側やマイナス側になっている可能性が高いです。 トレンドが大きくても、単独の場合は、母分散が大きくなっている可能性が高いです。
時系列分析の文献で、「実際の株価の変動は、（母数一定の）ランダムウォークモデルとは異なる」という説明は見かけることがあるのですが、それ以上詳しい説明を筆者見たことがないです。
もしも、実際の株価の変動が（母数一定の）ランダムウォークモデルと似ているのなら、「複数の会社が、同じような変化をする」という現象は、「偶然」という解釈になります。 ところが、実際には、あまりにも頻繁にそういった現象が起きるので、「偶然」とは考えにくいです。
一方、母平均変動型ランダムウォークモデルを仮定するのなら、「母平均が変わったから」や「母平均に関係する因子に変化があったから」と解釈できるようになります。
ランダムウォークモデルでは解釈できない現象については、外乱のようにして解釈されることが多いようですが、母平均変動型を使えば、モデルの中で解釈できるので、こちらの方が良さそうです。
上記の説明では、母数を決めてシミュレーションした例を説明しています。 現実には、母数は未知なので、データから母数を推定する分析をすることになります。
母分散変動型ランダムウォークモデルについては、 ボラティリティ推定モデル として、先行研究の文献を見かけます。
母平均も変動する場合については、筆者は見かけたことがないのですが、このサイトでは、筆者が考案した トレンド修正付きボラティリティ推定モデル （TSES-V）を説明しています。 TSES-Vを使うと、上記のようなデータから、母数を推定できます。
順路
次は
異常のモデル
