 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
高次元を2次元に圧縮する方法 を比較してみました。
主成分分析 (PCA) 、 多次元尺度構成法 (MDS) 、 自己組織化マップ (SOM)、t-SNE、UMAP、LLE、 高次元データのネットワーク分析 (NetworkMDS)を使った例になります。
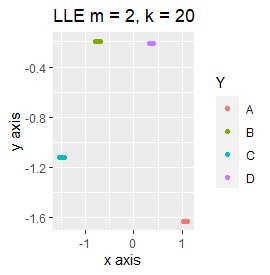
PCAは、第1、第2主成分だけを見ています。 MDSは、sammonを使っています。 NetworkMDSは、サンプルが増えて来ると、グラフの描画に非常に時間がかかったり、グラフが読み取れなくなったりするので、下記の事例で、サンプル数が多いものでは実施していません。 LLEは、2次元にしたいのでm=2です。kは収束するクラスターの数に相当するもので、大きくすると、計算時間がかかりますが、大は小を兼ねるので、ここでは20で大きめにしています。 t-SNEはパラメタの調整でいろいろ変わりますので、あくまで一例です。 UMAPで何も書いていないものは、n_neighborsがデフォルトです。 n_neighborsを変えると結果が良くなるものについては、一番良さそうな時のn_neighborsとしてグラフを作っています。
LLEとSOMは、うまく分かれると同じ座標に複数のサンプルが重ねるので、少し散らして、集まっている様子を見やすくしています。
あくまで、下記の事例からということになりますが、結論は2点です。
(1,2,3)、(4,5,6)、(7,8,9)、(10,11,12)が、それぞれ近くなっていてグループになっています。
大きな差はありません。
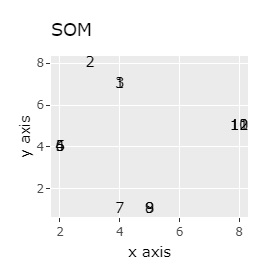
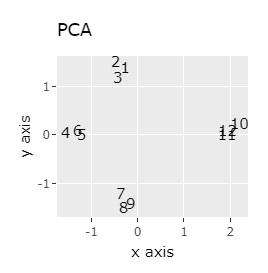
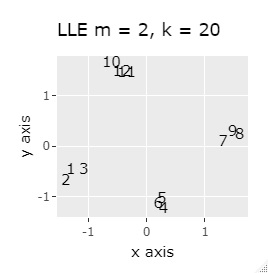
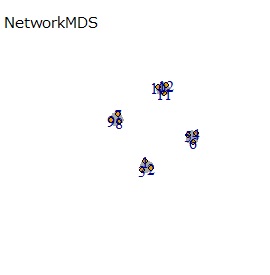
例1-1は、1つのグループは3個でしたが、例1-2では1つのグループは96個あります。
同じ色のサンプルは、元のグループが同じです。
どの例も、色の領域が明確に分かれていて良い結果でした。
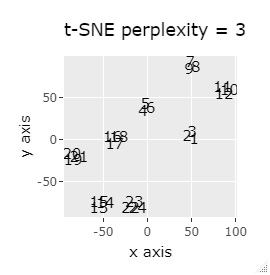
t-SNEは、パラメタの調整によっては、うまく分かれません。
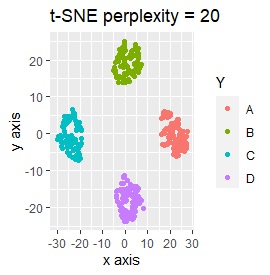

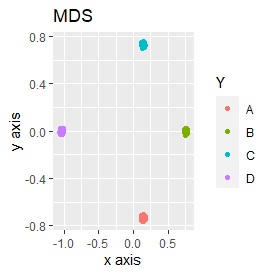
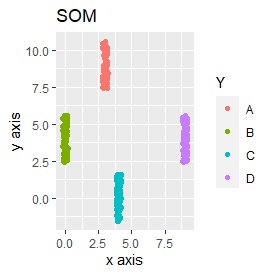
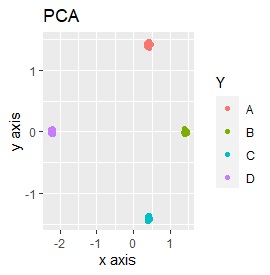
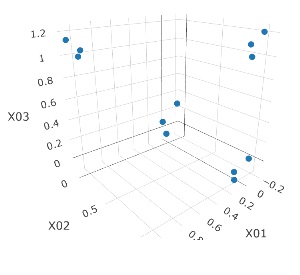
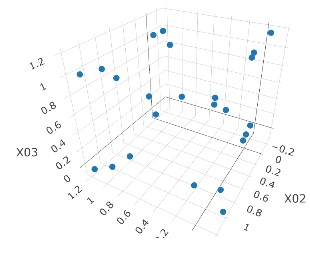
3次元のデータです。 立方体の頂点付近に、3個ずつサンプルのあるデータです。
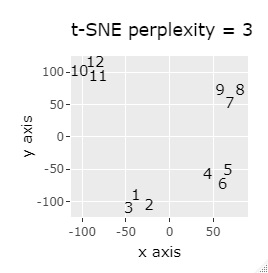
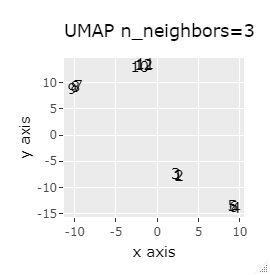
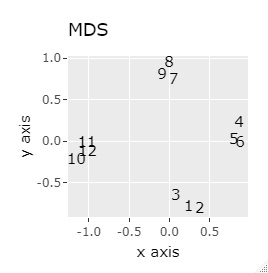
(1,2,3)、(4,5,6)、(7,8,9)、(10,11,12)、 (13,13,15)、(16,17,18)、(19,20,21)、(22,23,24)が、それぞれ近くなっていてグループになっています。
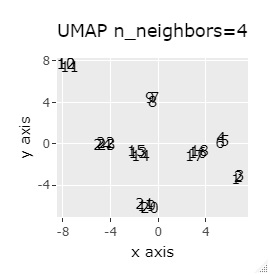
8つのグループを明確に分けることを目標とすれば、目標を達成できたのは、t-SNE、UMAP、NetworkMDSでした。
それ以外は、大きな間違いはなく、分かれてはいるのですが、明確ではない感じになりました。

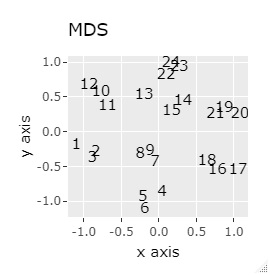
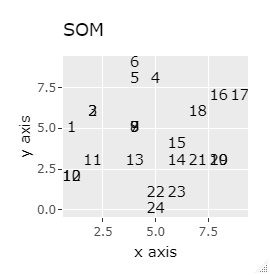
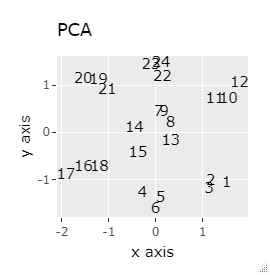
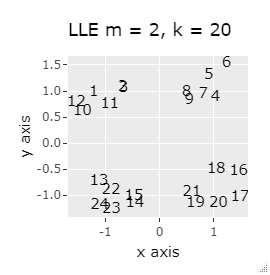
例2-1は、1つのグループは3個でしたが、例1-2では1つのグループは48個あります。
同じ色のサンプルは、元のグループが同じです。
PCAとSOM以外は、良い感じになりました。 PCAとSOMは、2つのグループが混ざりました。
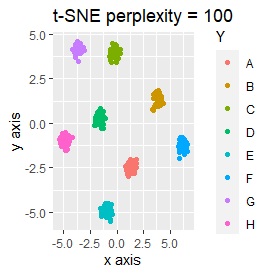
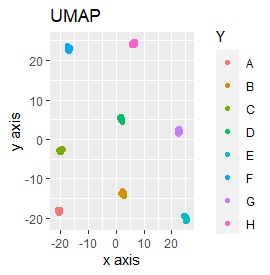
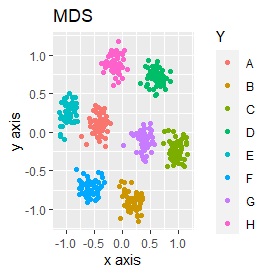
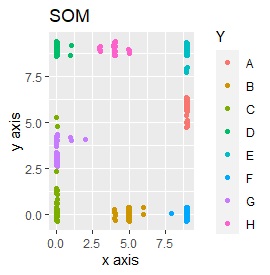
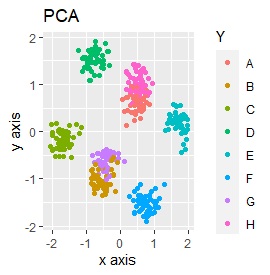
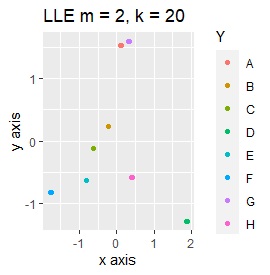
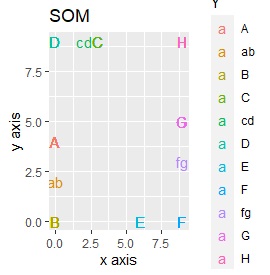
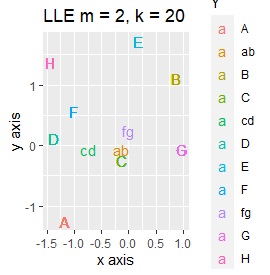
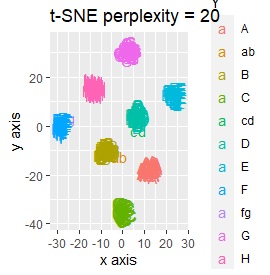
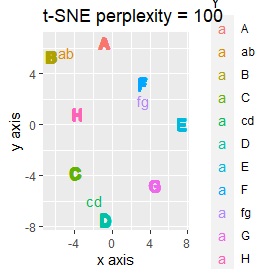
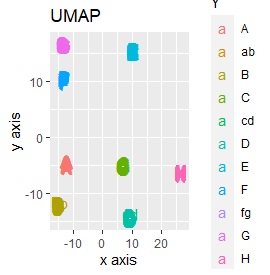
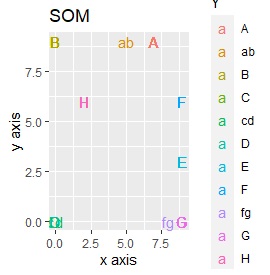
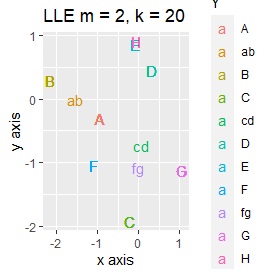
例2-2のグループに、3つのサンプルを足しています。 AとBの中間にab、CとDの中にcd、FとGの中間fgというサンプルが、1つずつあります。
t-SNEのperplexityを100、SOMについては、AとBの中間にab、CとDの中間にcd、FとGの中間にfgが配置され、理想的な結果になりました。
LLEも、AとBの中間にab、CとDの中間にcd、FとGの中間にfgという点では良いのですが、中間のabとfgが近くに配置されるのは理想的ではなかったです。
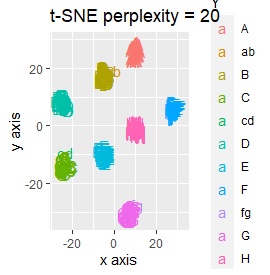
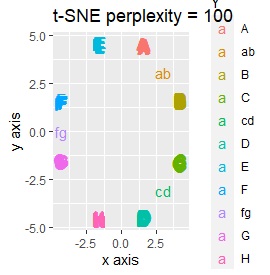

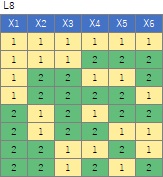
L8の 直交表 で作った6次元のデータです。 各水準にサンプルが2個ずつあり、その2個は少し離れています。
(1,2)、(3,4)、(5,6)、(7,8)、(9,10)、(11,12)、(13,14)、(15,16)が、それぞれ近くなっていてグループになっています。
8つのグループを明確に分けることを目標とすれば、目標を達成したのは、t-SNE、NetworkMDS、MDSでした。 それ以外は、大きな間違いはないですが、あいまいな分け方になりました。
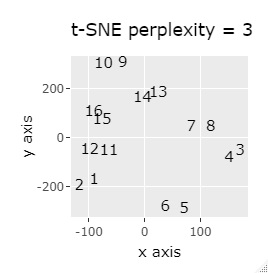
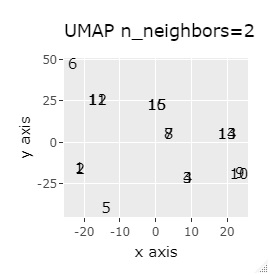
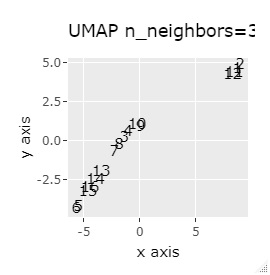
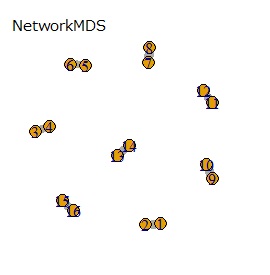
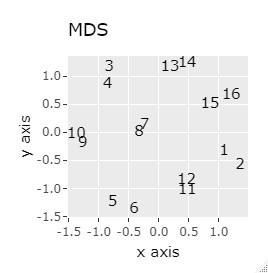
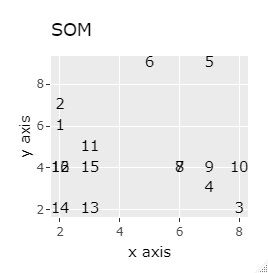
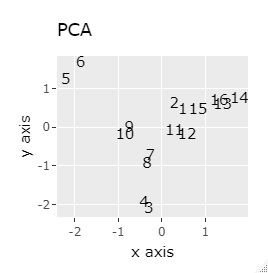
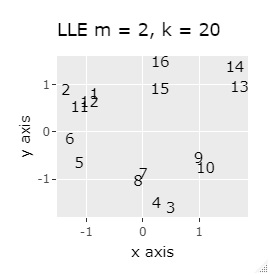
例3-1は、1つのグループは2個でしたが、例1-2では1つのグループは64個あります。
PCAとMDS以外は、うまく分かれました。
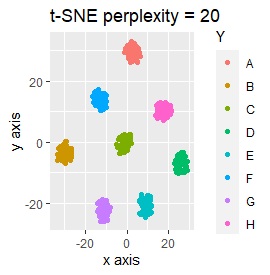
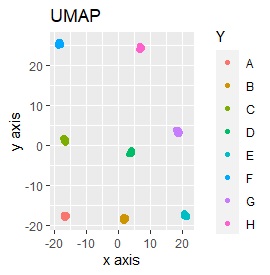
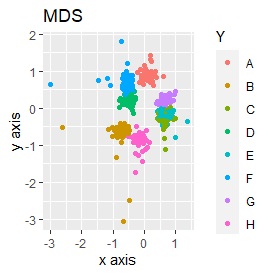
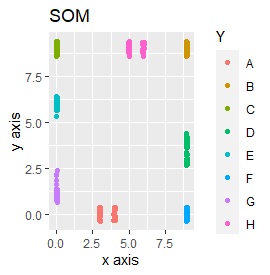
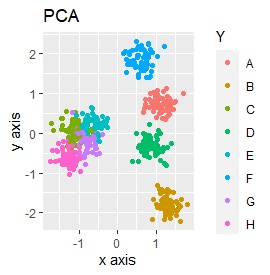
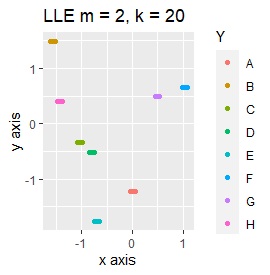
例3-2のグループに、3つのサンプルを足しています。 AとBの中間にab、CとDの中にcd、FとGの中間fgというサンプルが、1つずつあります。
t-SNEで、perplexityを100にしたものだけが、中間のサンプルが中間地点に来ませんでしたが、だいたい理想的な理想的な配置になりました。
SOMは、CとDがなぜか同じ位置に配置され、cdもそこに来ました。
LLEは、AとBの中間にab、CとDの中間にcd、FとGの中間にfgということは、確かに表せているのですが、cdとfgは近い、ということが起きています。 また、EとHが近くになっている点が理想的ではないです。
2次元空間に、3つのグループがあって、はっきり分かれている場合です。
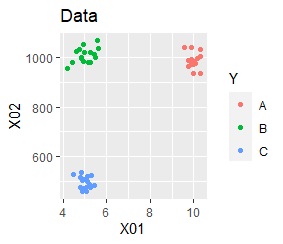
PCAとMDSは、3つにきれいに分かれました。 PCAとMDS以外は、2つに分かれました。 2次元を2次元に変換するので、どんな方法でも3つにうまく分かれそうな気もしますが、そうでもない例になります。
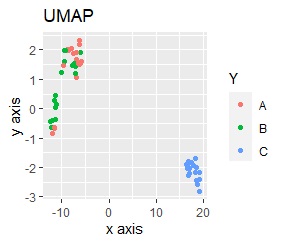
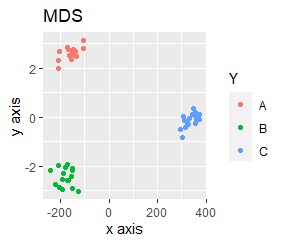
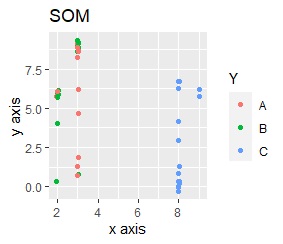
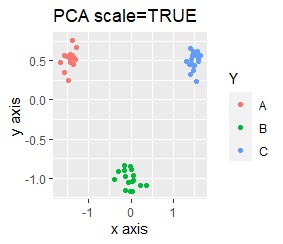
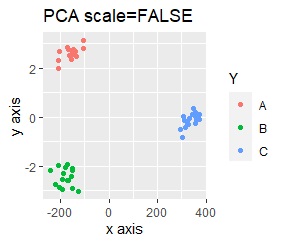
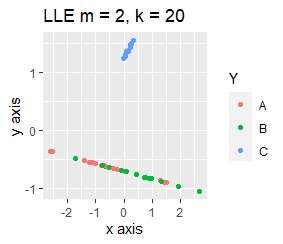

このデータのポイントは、X軸とY軸でスケールが桁違いな点になります。 MDSとPCAは、2次元の散布図で見えている配置が維持されているので、変換後の散布図で大きな違いが起きていません。
一方、PCAとMDS以外では、スケールの影響が大きく出ます。
PCAとMDS以外で、スケールの違いを出さない分析をするには、
スケール変換(
標準化や正規化
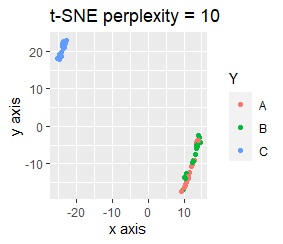
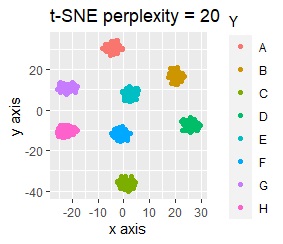
)をします。例えば、正規化をしてからt-SNEをすると、下図になり、3つのグループにきれいに分かれています。
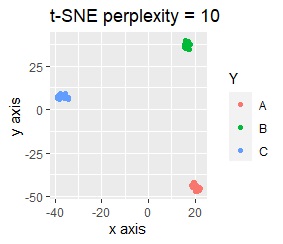
次元削減の手法を勉強する時の題材は、2次元や3次元の位置座標のデータになっていることが普通です。 そういったデータだと、この例のようなことは起きにくいです。
一方、実際のデータ分析では、単位が異なる変数が混ざっていることがあり、この例のようなことを気にする必要があります。 ただし、正規化をすると、元のデータが持っていた物理的な意味がなくなります。 そのため、単純に「正規化を前処理に必ず入れましょう」とはならないのが、このケースの難しさになっています。
例3-1のデータとほぼ同じなのですが、ひとつの変数(次元)だけ値が桁違いになっている場合です。
このデータの場合、例3-1と例4-1の両方の話が入って来て、8つのグループを分けられる方法はひとつもありませんでした。
面白いのは、例3-1で良くない結果が出たように見えたPCAとMDSが、この例では、そこそこ良い方法になっているところです。 高次元を2次元で見る方法として、一般論としては、PCAとMDSはあまり良い方法ではないです。 コレスポンデンス分析 もそうです。 しかし、高次元の中に、範囲の狭いグループが点在しているような時は、 空間をうまく回転することで、2次元の中に、点在しているものがうまく分かれて配置できることがあります。 t-SNEやSOMが開発される前から、これらの分析方法がそれなりに役に立って来た理由は、この点にあるのかもしれません。
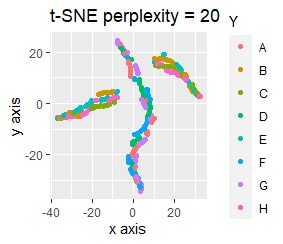
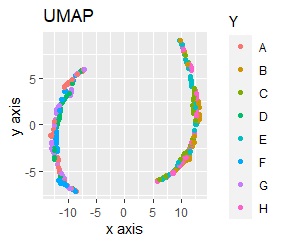
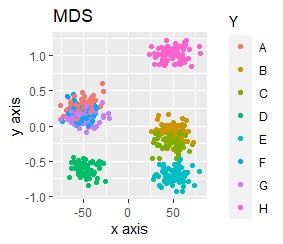
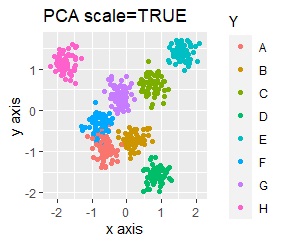
例えば、正規化をしてからt-SNEをすると、下図になります。8つのグループにきれいに分かれています。
Rによる実施例は、 Rによる高次元を2次元に圧縮して可視化 にまとまっています。
R-EDA1
では、MDS、t-SNE、UMAP、NetworkMDSをできるようにしてあります。
「Python実践AIモデル構築100本ノック」 下山輝昌・中村智・高木洋介 著 秀和システム 2021
様々な手法について、使い方がコンパクトにまとまっています。
次元削減の方法として、下記が紹介されています。
PCA:
Isomap:多様体上の距離を測定して、多次元尺度構成法をする。近いもの同士の特徴が多次元尺度構成法よりも表しやすい。
t-SNE:
UMAP:t-SNEと結果が似ているが、パラメタ調整が簡単。n_neighborsを調整すると、ミクロな構造とマクロな構造の反映の仕方を調整できる。デフォルトは15。
著者のおすすめはPCAとUMAPで、いずれも良くない時にt-SNEを試す使い方。
ALBERT社のブログ
スイスロールのデータを使って、様々な手法を比較した例が載っています。
https://blog.albert2005.co.jp/2014/12/11/%E9%AB%98%E6%AC%A1%E5%85%83%E3%83%87%E3%83%BC%E3%82%BF%E3%81%AE%E5%8F%AF%E8%A6%96%E5%8C%96%E3%81%AE%E6%89%8B%E6%B3%95%E3%82%92swiss-roll%E3%82%92%E4%BE%8B%E3%81%AB%E8%A6%8B%E3%81%A6%E3%81%BF%E3%82%88/
「Pythonではじめる教師なし学習 機械学習の可能性を広げるラベルなしデータの利用」 Ankur A. Patel 著 中田秀基 訳 オライリー・ジャパン 2020
次元削減として、PCA(
主成分分析
)、
特異値分解
、ランダム射影、Isomap、MDS(
多次元尺度構成法
)、LLE(局所線形埋め込み)、t-SNE、辞書学習、ICA(
独立成分分析
)が紹介されています。
「Pythonではじめる機械学習 scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎」 Andreas C.Muller, Sarah Guido 著 オライリー・ジャパン 2017
Pythonを使った機械学習について、具体的な話がコンパクトにまとまっています。
多様体学習アルゴリズムの中でも特に有用なものとして、t-SNEを紹介しています。
t-SNEの場合、デフォルトのパラメータの設定で大抵はうまく行くそうです。
順路


 次は
距離の関係を保って2次元に圧縮する方法
次は
距離の関係を保って2次元に圧縮する方法

