変数の意味を使って２次元に圧縮する方法

高次元を２次元に圧縮して可視化の一般的なアプローチは、「高次元」というところに注目するだけで、高次元の内訳は気にしない手法になっています。

もしも、高次元の中に、２種類に分けられる内訳があるのなら、それを活用した方が、見通しの良い分析になります。

高次元の中の内訳

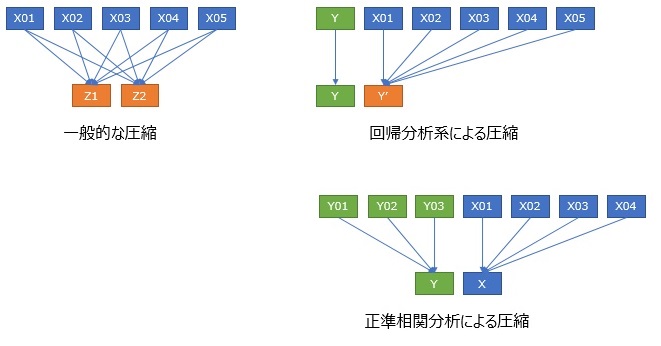
２種類の内訳が、一対多になる場合と、多対多になる場合があります。

一対多になる場合は、目的変数と説明変数に分けられる場合があります。説明変数側が「多」になります。回帰分析系で高次元を２次元に圧縮は、この系統です。

多対多になる場合は、原因系と結果系に分けられる場合があります。正準相関分析で高次元を２次元に圧縮は、この系統です。