回帰分析系で高次元を２次元に圧縮 の場合は、目的変数とその他の変数に分けます。 このページの方法は、目的変数が変数のグループになっている場合と解釈することができます。
回帰分析系では、１つの変数と複数の変数の関係を扱いますが、このページの方法では、複数同士の関係です。
これができる方法は、
正準相関分析
です。
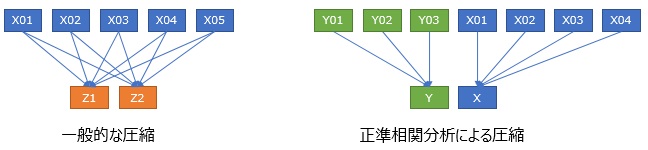
正準相関分析 を 、高次元を２次元に圧縮して可視化 の方法に応用します。
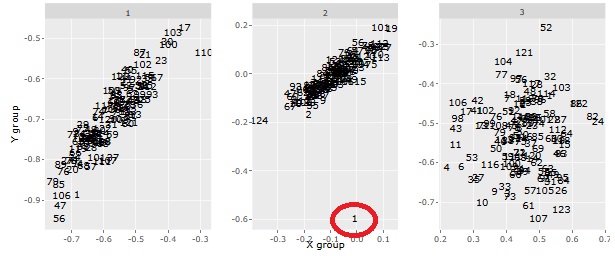
下の例は、左から順にが第１成分同士の散布図、第２成分同士の散布図、第３成分同士の散布です。 使っているデータは、１行目のサンプルだけ、他のサンプルとは違って適当に入れた値を使っているのですが、真ん中の散布図の方で、このサンプルが外れているのが見えています。 また、３つの因子がありますが、２つのグループで相関の高い因子は２種類しかないことがわかります。
高次元を２次元に圧縮して可視化
の方法は、散布図が１枚で分析するのが普通ですが、正準相関分析を使う場合、２枚以上見ないとわからない例になっています。
Rによる正準相関分析 のページには、カーネル法を使った非線形の正準相関分析も載せましたが、まだ、実務で役立ちそうな分析例に、筆者は出会ったことがないです。
R-EDA1では、非線形の正準相関分析もできます。
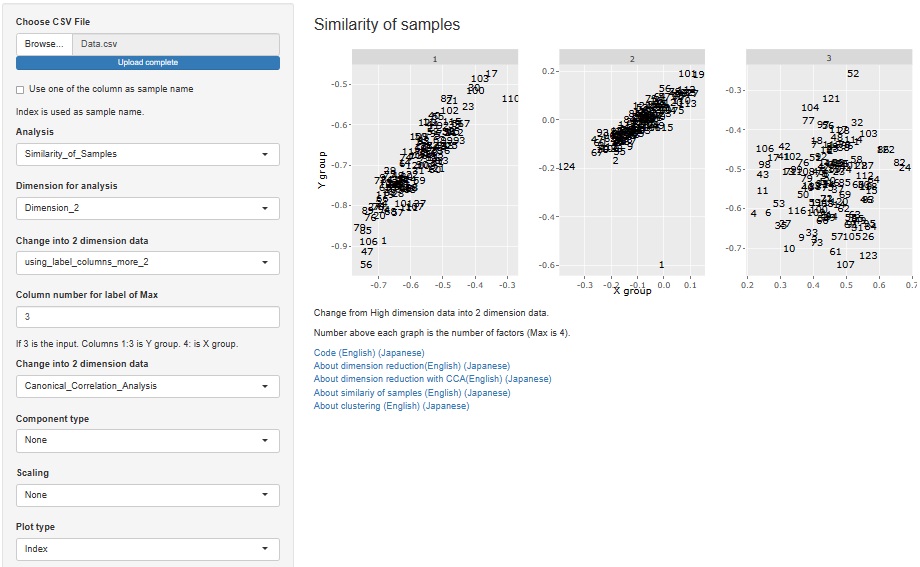
Rによる正準相関分析のページがあります。
順路
次は
クラスター分析
