Rによる正準相関分析
正準相関分析
や
正準相関分析で高次元を２次元に圧縮
のRによる実施例です。
下記は、コードのメモとして書いたもので、「分析」というほど、詳しくないです。
普通の正準相関分析
例のデータは、変数は６個あり、左から３個までと、それ以降の３個のそれぞれが群と想定しています。
主成分分析が、第１主成分、第２主成分というように、複数の合成変数が計算されるのと同じように、正準相関分析でも複数の合成変数が計算されます。
下記の例では、第１成分の組合せだけを抽出して、散布図にしています。
CCAライブラリ
setwd("C:/Rtest")
library(CCA)
library(ggplot2)
library(plotly)
Data <- read.csv("Data.csv", header=T)
Retu <- 3 # 1列目から3列目までがひとつの群で、4列目以降がもうひとつの群になる。
DataX <- Data[,1:Retu]
Retu2 <- Retu+1
Retu3 <- ncol(Data)
DataY <- Data[,Retu2:Retu3]
model <- cc(DataX,DataY)# 正準相関分析
Youso <- 1# グラフにする成分の番号
X1 <- model$scores$xscores[,Youso]
Y1 <- model$scores$yscores[,Youso]
Data5 <- cbind(data.frame(X1,Y1),Index = row.names(Data))
ggplotly(ggplot(Data5, aes(x=X1, y=Y1,label=Index)) + geom_text() + labs(x="Xs",y="Ys"))# 行番号がプロットされる
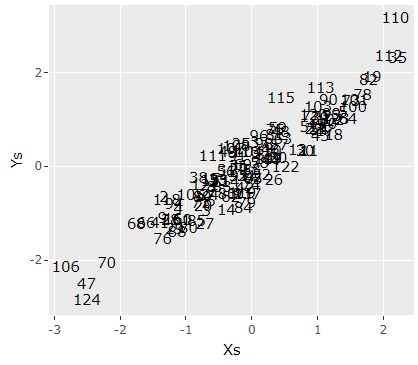
model$cor# 相関係数を出力
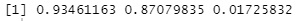
第１成分同士は、相関係数が0.93あることがわかります。
第２成分同士も、0.87なので高めです。
cancor関数
cancor関数は、Rに標準的にインストールされています。基本的にCCAと使い方は同じですが、新しい成分は計算されないので、係数から計算する必要があります。
setwd("C:/Rtest")
library(ggplot2)
library(plotly)
Data <- read.csv("Data.csv", header=T)
Retu <- 3 # 1列目から3列目までがひとつの群で、4列目以降がもうひとつの群になる。
DataX <- Data[,1:Retu]
Retu2 <- Retu+1
Retu3 <- ncol(Data)
DataY <- Data[,Retu2:Retu3]
model <- cancor(DataX,DataY)# 正準相関分析
u <- data.matrix(DataX) %*% model$xcoef
v <- data.matrix(DataY) %*% model$ycoef
Data6 <- cbind(u = data.frame(u[,1]),v = data.frame(v[,1]),Index = row.names(Data),Factors = c(1))
names(Data6)[1:2] <- c("u","v")
for(i in 2:min(ncol(u),ncol(v))) {
Data61 <- cbind(u = data.frame(u[,i]),v = data.frame(v[,i]),Index = row.names(Data),Factors = c(i))
names(Data61)[1:2] <- c("u","v")
Data6 <- rbind(Data6,Data61)
}
ggplot(Data6, aes(x=u,y=v,label=Index)) + geom_text() + facet_wrap(~Factors,scales="free") + labs(x="Xs",y="Ys")
カーネル正準相関分析（非線形）
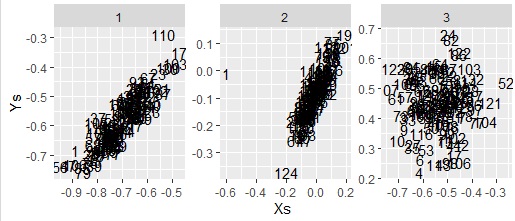
例のデータは、変数は６個あり、左から３個までと、それ以降の３個のそれぞれが群と想定しています。
kernlabライブラリ
setwd("C:/Rtest")
library(kernlab)
library(ggplot2)
library(plotly)
Data <- read.csv("Data.csv", header=T)
Retu <- 3 # 1列目から3列目までがひとつの群で、4列目以降がもうひとつの群になる。
DataX <- Data[,1:Retu]
Retu2 <- Retu+1
Retu3 <- ncol(Data)
DataY <- Data[,Retu2:Retu3]
k <- rbfdot()# laplacedot(), besseldot(), anovadot(), splinedot(), polydot(), vanilladot(), tanhdot()
result <- kcca(data.matrix(DataX), data.matrix(DataY), kernel = k, ncomps = 3)
u <- kernelMatrix(k,data.matrix(DataY)) %*% result@xcoef
v <- kernelMatrix(k,data.matrix(DataX)) %*% result@ycoef
Youso <- 1# グラフにする成分の番号
Y1 <- u[,Youso]
X1 <- v[,Youso]
Data5 <- cbind(data.frame(X1,Y1),Index = row.names(Data))
ggplotly(ggplot(Data5, aes(x=X1, y=Y1,label=Index)) + geom_text() + labs(x="Xs",y="Ys"))# 行番号がプロットされる
参考文献
「CCA」
CRANにあるCCAのマニュアルです。
https://cran.r-project.org/web/packages/CCA/CCA.pdf
「正準相関分析入門」
論文です。cancorとkernlabの使用例があります。
https://www.jstage.jst.go.jp/article/jnns/20/2/20_62/_pdf
