トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

残差の外れ値

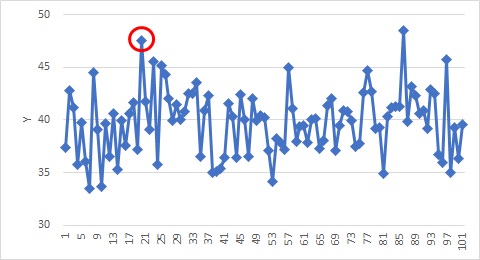
このページで扱うのは、上の図のようなデータの中にある異常値になります。 先に正解を書くと、赤丸のデータだけが異常値です。 赤丸のついていないデータで、赤丸のデータよりも高いデータがありますが、これは異常値ではありません。

このデータは、 時系列データの異常値 のページの方法を使ったとしても、「異常」をあぶり出すことができません。

この例は、この中に、原因系が外れているが、結果系であるデータは外れていない場合になります。 そのため、このデータを見る限りでは、「外れ」はありません。

残差の外れ値の使い道

「原因系が外れているが、結果系であるデータは外れていない場合」の例としては、例えば、 「何からの不正やミスによって、本来なら外れ値となるはずだったのに、データは正常値になっている場合」があります。 そのため、このページの方法は、不正やミスの検知の方法になります。

前提条件

上の図のデータしかなければ、どうやっても、異常値かどうかは判断できません。

このページの方法を使うには前提条件があり、Y以外のデータが必要です。 そして、YとY以外のデータで、関係式が作れる必要があります。

関係式の作り方は、特に条件がありません。 このページの例は、 回帰分析 ですが、 回帰木 や サポートベクター回帰 など、目的変数が量的データになっている教師あり学習のモデルなら、何でも使えます。

残差

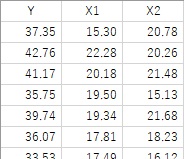
残差は、予測値と実測値の差です。

例えば、
Y = X1 + X2
という関係式を作った場合に、X1とX2をこの式に入れて求まる値が予測値（Y'）で、元のデータのYが実測値です。

ちなみに、 回帰分析 では、残差が最小になるようにモデル式の係数を計算します。

残差の外れ値の分析

上の図の例で残差を求めると、下の図になります。

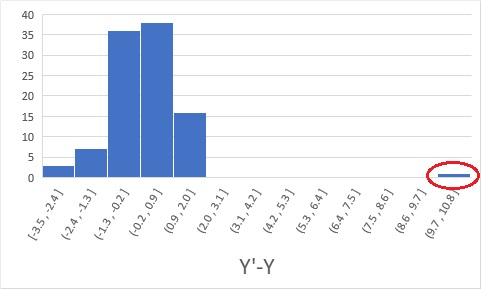
赤丸のデータの残差は、外れ値として計算されています。 こうすることで、異常値としてあぶり出すことができました。

Y'とYの両方が正常値だとしても、Y'とYの差（残差）は異常になっている点がポイントです。 異常値の調査として、Yを調べることは、初歩的なデータ分析です。 Y'も調べることは、それよりもレベルの高いデータ分析です。 Y'とYの差も調べることは、さらにレベルの高いデータ分析かと思います。

残差のモデルの作り方のノウハウ

上の図の例のように、すでにデータがあって、「この中に不正のデータがあるかもしれない」と調べたい場合は、 回帰分析 などの、 教師あり学習 のモデルで一番当てはまりの良いものを選び、残差の分布をみる手順になります。

別の場合として、「このデータが不正かどうかを調べたい」、「新しいデータが不正かをチェックしたい」といった場合は、ノウハウがあります。

チェックしたいデータも含めたすべてのデータでモデルを作ってから、チェックしたいデータの残差を調べるのではなく、 「正常」と考えているデータだけでモデルを作ってから、チェックしたいデータをそのモデルに入力して、残差を調べるようにします。

こうすることで、異常のデータが含まれている場合に、モデルの作成にこのデータが含まれていると、モデルの中にうまく入ってしまい、「外れ値」としての値が小さくなりやすくなるのを防止する効果があります。 また、異常のデータが含まれていると、モデルの精度が悪くなり、「モデルができない」という可能性もあるので、これを防止する効果があります。

ちなみに、このノウハウは、 1クラスモデル の考え方と似ています。 また、残差の大きさで異常をあぶり出す方法は、 オートエンコーダー による異常検知と似ています。 このページの方法と、これらの方法の違いは、目的変数が量的データになっている点が違います。

ソフト

Excel

Excelでは、回帰分析の残差を、簡単に分析できます。上の例もExcelでしています。 Excelによる残差の外れ値の分析 のページがあります。

R-EDA1

R-EDA1でもできます。 ヒストグラムが残差の分布になっています。

上の場合は、回帰分析ですが、 モデル木 や サポートベクター回帰 も使えます。

R

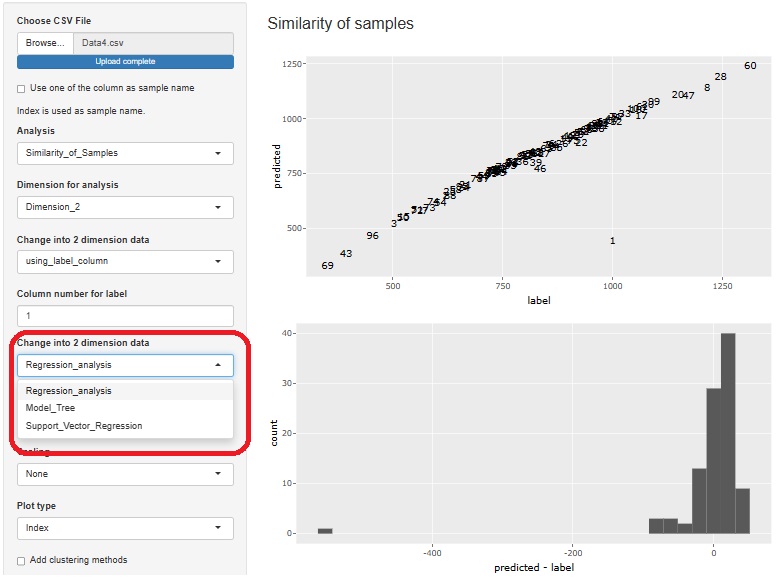
Rによる回帰分析系で高次元を２次元に圧縮して可視化 では、 R-EDA1に入れているコードの中心になっているものが入っています。

順路 次は 測定