時系列データの異常値

外れ値ではない異常値のモデルは、正常をどのように定義するかがポイントですが、時系列の情報があるデータだと、その情報を活用できます。

自己単相関のモデル

自己単相関がある場合は、あるデータと、「1ステップ前のデータ」や「1ステップ後のデータ」が近い場合です。

例えば、下図のようなデータで見える異常は、「1ステップ前のデータ」との差を計算すると、外れ値として扱うことができるようになります。
異常値

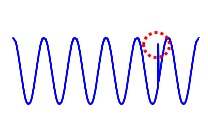
上記のようなデータの場合は、「SINカーブ」と仮定することができます。この場合は、「SINカーブだったら、この時はこの値になるはず」という予測値が計算できます。

異常と思っているところ以外は、この予実差が小さな値になり、異常と思っているところは大きくなりますので、外れ値の判定方法が使えるようになります。

「異常が変数間の関係性の変化に表れている」という異常があります。例えば、「普段は、相関のない２つの変数が、異常の時は相関している」という場合です。

こうした異常の場合は、1行単位でバラバラに処理する方法では、異常性がうまく表現できない事があります。

このような場合は、移動分析を使って、関係性のデータを作ると、関係性の外れとして、外れ値の判定方法が使えるようになります。

伝統的に、品質学の分野では、 SPC（統計的工程管理）が発達しています。

その手法のひとつの管理図では、ひとつの変数について、異常状態の検知の仕方が定められています。

考え方としては、値の増減の仕方が同じ母集団から発生したものと言えるかどうかで判断します。

外れ値もその一種ですが、その他にもいろいろな種類の異常が考案されています。「平均値よりも高い場合が、連続する」、「平均値の上下を行ったり来たりする」といったものです。